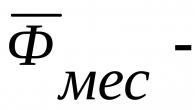V tomto materiáli sa pozrieme na to, ako nájsť rovnicu roviny, ak poznáme súradnice troch rôznych bodov, ktoré neležia na rovnakej priamke. Aby sme to dosiahli, musíme si pamätať, čo je pravouhlý súradnicový systém v trojrozmernom priestore. Na začiatok si predstavíme základný princíp tejto rovnice a ukážeme si, ako presne ju použiť na riešenie konkrétnych problémov.

Yandex.RTB R-A-339285-1

Najprv si musíme zapamätať jednu axiómu, ktorá znie takto:

Definícia 1

Ak sa tri body navzájom nezhodujú a neležia na rovnakej priamke, potom v trojrozmernom priestore nimi prechádza iba jedna rovina.

Inými slovami, ak máme tri rôzne body, ktorých súradnice sa nezhodujú a ktoré nemožno spojiť priamkou, potom môžeme určiť rovinu, ktorá cez ne prechádza.

Povedzme, že máme pravouhlý súradnicový systém. Označme to O x y z. Obsahuje tri body M so súradnicami M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3), ktoré nemožno spojiť. priamka. Na základe týchto podmienok môžeme zapísať rovnicu roviny, ktorú potrebujeme. Existujú dva prístupy k riešeniu tohto problému.

1. Prvý prístup používa všeobecnú rovinnú rovnicu. V listovej forme sa píše ako A (x - x 1) + B (y - y 1) + C (z - z 1) = 0. S jeho pomocou môžete definovať v pravouhlom súradnicovom systéme určitú alfa rovinu, ktorá prechádza prvým daným bodom M 1 (x 1, y 1, z 1). Ukazuje sa, že normálny vektor roviny α bude mať súradnice A, B, C.

Definícia N

Keď poznáme súradnice normálového vektora a súradnice bodu, ktorým rovina prechádza, môžeme zapísať všeobecnú rovnicu tejto roviny.

Z toho budeme v budúcnosti vychádzať.

Teda podľa podmienok úlohy máme súradnice požadovaného bodu (aj troch), ktorým rovina prechádza. Ak chcete nájsť rovnicu, musíte vypočítať súradnice jej normálneho vektora. Označme to n → .

Zapamätajme si pravidlo: každý nenulový vektor danej roviny je kolmý na normálový vektor tej istej roviny. Potom máme, že n → bude kolmé na vektory zložené z pôvodných bodov M 1 M 2 → a M 1 M 3 → . Potom môžeme označiť n → ako vektorový súčin tvaru M 1 M 2 → · M 1 M 3 → .

Pretože M 1 M 2 → = (x 2 - x 1, y 2 - y 1, z 2 - z 1) a M 1 M 3 → = x 3 - x 1, y 3 - y 1, z 3 - z 1 (dôkazy týchto rovnosti sú uvedené v článku venovanom výpočtu súradníc vektora zo súradníc bodov), potom sa ukazuje, že:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1

Ak vypočítame determinant, získame súradnice normálového vektora n → potrebujeme. Teraz môžeme napísať rovnicu, ktorú potrebujeme pre rovinu prechádzajúcu tromi danými bodmi.

2. Druhý prístup k hľadaniu rovnice prechádzajúcej cez M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3), je založený na takom koncepte, ako je koplanarita vektorov.

Ak máme množinu bodov M (x, y, z), tak v pravouhlom súradnicovom systéme definujú rovinu pre dané body M 1 (x 1, y 1, z 1), M 2 (x 2, y 2 , z 2 ), M 3 (x 3 , y 3 , z 3) len v prípade, že vektory M 1 M → = (x - x 1 , y - y 1 , z - z 1), M 1 M 2 → = (x 2 - x 1, y 2 - y 1, z 2 - z 1) a M 1 M 3  → = (x 3 - x 1, y 3 - y 1, z 3 - z 1) budú koplanárne .

V diagrame to bude vyzerať takto:

To bude znamenať, že zmiešaný súčin vektorov M 1 M → , M 1 M 2 → , M 1 M 3 → sa bude rovnať nule: M 1 M → · M 1 M 2 → · M 1 M 3 → = 0 , keďže toto je hlavná podmienka koplanarity: M 1 M → = (x - x 1, y - y 1, z - z 1), M 1 M 2 → = (x 2 - x 1, y 2 - y 1 z2 - zi) a M1M3 -> = (x3 - x 1, y3 - y1, z3 - zi).

Napíšme výslednú rovnicu v súradnicovom tvare:

Po vypočítaní determinantu môžeme získať rovinnú rovnicu, ktorú potrebujeme pre tri body, ktoré neležia na rovnakej priamke M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2) M3 (x3, y3, z3).

Z výslednej rovnice môžete prejsť na rovnicu roviny v segmentoch alebo na normálnu rovnicu roviny, ak si to podmienky úlohy vyžadujú.

V nasledujúcom odseku uvedieme príklady, ako sa v praxi nami uvedené prístupy implementujú.

Príklady úloh na zostavenie rovnice roviny prechádzajúcej 3 bodmi

Predtým sme identifikovali dva prístupy, ktoré možno použiť na nájdenie požadovanej rovnice. Pozrime sa, ako sa používajú na riešenie problémov a kedy by ste si mali vybrať jednotlivé.

Príklad 1

Existujú tri body, ktoré neležia na tej istej priamke, so súradnicami M 1 (- 3, 2, - 1), M 2 (- 1, 2, 4), M 3 (3, 3, - 1). Napíšte rovnicu pre rovinu, ktorá nimi prechádza.

Riešenie

Striedavo používame oba spôsoby.

1. Nájdite súradnice dvoch vektorov, ktoré potrebujeme M 1 M 2 →, M 1 M 3 →:

M 1 M 2 → = - 1 - - 3, 2 - 2, 4 - - 1 ⇔ M 1 M 2 → = (2, 0, 5) M 1 M 3 → = 3 - - 3, 3 - 2, - 1 -- 1 ⇔ M 1 M 3 → = 6 , 1 , 0

Teraz vypočítajme ich vektorový súčin. Nebudeme popisovať výpočty determinantu:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = - 5 i → + 30 j → + 2 k →

Máme normálový vektor roviny, ktorý prechádza cez tri požadované body: n → = (- 5, 30, 2) . Ďalej musíme vziať jeden z bodov, napríklad M 1 (- 3, 2, - 1), a zapísať rovnicu pre rovinu s vektorom n → = (- 5, 30, 2). Dostaneme, že: - 5 (x - (- 3)) + 30 (y - 2) + 2 (z - (- 1)) = 0 ⇔ - 5 x + 30 y + 2 z - 73 = 0

Toto je rovnica, ktorú potrebujeme pre rovinu, ktorá prechádza tromi bodmi.

2. Zoberme si iný prístup. Napíšme rovnicu pre rovinu s tromi bodmi M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) v nasledujúci formulár:

x - x 1 r - y 1 z - z 1 x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1 = 0

Tu môžete nahradiť údaje z výpisu problému. Pretože x 1 = - 3, y 1 = 2, z 1 = - 1, x 2 = - 1, y 2 = 2, z 2 = 4, x 3 = 3, y 3 = 3, z 3 = - 1, nakoniec dostaneme:

x - x 1 y - y 1 z - z 1 x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1 = x - (- 3) y - 2 z - (- 1) - 1 - (- 3) 2 - 2 4 - (- 1) 3 - (- 3) 3 - 2 - 1 - (- 1) = = x + 3 y - 2 z + 1 2 0 5 6 1 0 = - 5 x + 30 r + 2 z - 73

Dostali sme rovnicu, ktorú sme potrebovali.

odpoveď:- 5 x + 30 y + 2 z - 73.

Čo ak však dané body stále ležia na tej istej priamke a potrebujeme pre ne vytvoriť rovinnú rovnicu? Tu treba hneď povedať, že táto podmienka nebude úplne správna. Takýmito bodmi môže prechádzať nekonečné množstvo rovín, preto nie je možné vypočítať jednu odpoveď. Uvažujme nad takýmto problémom, aby sme dokázali nesprávnosť takejto formulácie otázky.

Príklad 2

Máme pravouhlý súradnicový systém v trojrozmernom priestore, v ktorom sú umiestnené tri body so súradnicami M 1 (5, - 8, - 2), M 2 (1, - 2, 0), M 3 (- 1, 1 , 1). Pre rovinu, ktorá cez ňu prechádza, je potrebné napísať rovnicu.

Riešenie

Využime prvý spôsob a začnime výpočtom súradníc dvoch vektorov M 1 M 2 → a M 1 M 3 →. Vypočítajme ich súradnice: M 1 M 2 → = (- 4, 6, 2), M 1 M 3 → = - 6, 9, 3.

Krížový produkt sa bude rovnať:

M 1 M 2 → × M 1 M 3 → = i → j → k → - 4 6 2 - 6 9 3 = 0 i ⇀ + 0 j → + 0 k → = 0 →

Keďže M 1 M 2 → × M 1 M 3 → = 0 →, potom budú naše vektory kolineárne (ak ste zabudli na definíciu tohto pojmu, prečítajte si o nich znova článok). Počiatočné body M 1 (5, - 8, - 2), M 2 (1, - 2, 0), M 3 (- 1, 1, 1) sú teda na jednej priamke a náš problém má nekonečne veľa možnosti odpoveď.

Ak použijeme druhú metódu, dostaneme:

x - x 1 y - y 1 z - z 1 x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1 = 0 ⇔ x - 5 r - (- 8) z - (- 2) 1 - 5 - 2 - (- 8) 0 - (- 2) - 1 - 5 1 - (- 8) 1 - (- 2) = 0 ⇔ ⇔ x - 5 r. + 8 z + 2 - 4 6 2 - 6 9 3 = 0 ⇔ 0 ≡ 0

Z výslednej rovnosti tiež vyplýva, že dané body M 1 (5, - 8, - 2), M 2 (1, - 2, 0), M 3 (- 1, 1, 1) ležia na tej istej priamke. .

Ak chcete nájsť aspoň jednu odpoveď na tento problém z nekonečného množstva jeho možností, musíte postupovať podľa týchto krokov:

1. Napíšte rovnicu priamky M 1 M 2, M 1 M 3 alebo M 2 M 3 (v prípade potreby si pozrite materiál o tomto úkone).

2. Vezmite bod M 4 (x 4, y 4, z 4), ktorý neleží na priamke M 1 M 2.

3. Napíšte rovnicu roviny, ktorá prechádza tromi rôznymi bodmi M 1, M 2 a M 4, ktoré neležia na tej istej priamke.

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Rovnica roviny. Ako napísať rovnicu roviny?
Vzájomné usporiadanie rovín. Úlohy

Priestorová geometria nie je oveľa komplikovanejšia ako „plochá“ geometria a naše lety vo vesmíre začínajú týmto článkom. Na zvládnutie témy je potrebné, aby ste jej dobre rozumeli vektory Okrem toho je vhodné poznať geometriu roviny - bude tam veľa podobností, mnoho analógií, takže informácie budú oveľa lepšie strávené. V sérii mojich lekcií sa 2D svet otvára článkom Rovnica priamky na rovine. Teraz však Batman opustil plochú televíznu obrazovku a štartuje z kozmodrómu Bajkonur.

Začnime s kresbami a symbolmi. Schematicky môže byť rovina nakreslená vo forme rovnobežníka, ktorý vytvára dojem priestoru:

Rovina je nekonečná, no my máme možnosť znázorniť len jej kúsok. V praxi sa okrem rovnobežníka kreslí aj ovál či dokonca oblak. Z technických dôvodov je pre mňa pohodlnejšie znázorniť lietadlo presne takto a presne v tejto polohe. Skutočné lietadlá, ktoré budeme zvažovať v praktických príkladoch, môžu byť umiestnené akýmkoľvek spôsobom - mentálne vezmite kresbu do rúk a otočte ju v priestore, čím dáte rovine akýkoľvek sklon, akýkoľvek uhol.

Označenia: lietadlá sa zvyčajne označujú malými gréckymi písmenami, zrejme preto, aby si ich nepomýlili priamka na rovine alebo s priamka v priestore. Som zvyknutý používať písmeno . Na výkrese je to písmeno „sigma“ a vôbec nie diera. Aj keď, dierované lietadlo je určite celkom vtipné.

V niektorých prípadoch je vhodné použiť rovnaké grécke písmená s nižšími indexmi na označenie rovín, napríklad .

Je zrejmé, že rovina je jednoznačne definovaná tromi rôznymi bodmi, ktoré neležia na tej istej priamke. Preto sú pomerne obľúbené trojpísmenové označenia lietadiel - napríklad bodmi, ktoré k nim patria atď. Písmená sú často uzavreté v zátvorkách: , aby nedošlo k zámene roviny s iným geometrickým útvarom.

Pre skúsených čitateľov dám menu rýchleho prístupu:

• Ako vytvoriť rovnicu roviny pomocou bodu a dvoch vektorov?
• Ako vytvoriť rovnicu roviny pomocou bodu a normálového vektora?

a nebudeme sa zdržiavať dlhým čakaním:

Všeobecná rovinná rovnica

Všeobecná rovnica roviny má tvar , kde koeficienty sa zároveň nerovnajú nule.

Množstvo teoretických výpočtov a praktických problémov platí ako pre bežnú ortonormálnu bázu, tak aj pre afinnú bázu priestoru (ak je olej olej, vráťte sa k lekcii Lineárna (ne)závislosť vektorov. Základy vektorov). Pre jednoduchosť budeme predpokladať, že všetky udalosti sa vyskytujú na ortonormálnom základe a karteziánskom pravouhlom súradnicovom systéme.

Teraz si trochu precvičíme priestorovú predstavivosť. Je v poriadku, ak je ten váš zlý, teraz ho trochu rozvinieme. Aj hranie na nervy si vyžaduje tréning.

V najvšeobecnejšom prípade, keď sa čísla nerovnajú nule, rovina pretína všetky tri súradnicové osi. Napríklad takto:

Ešte raz opakujem, že rovina pokračuje donekonečna všetkými smermi a my máme možnosť znázorniť len jej časť.

Zoberme si najjednoduchšie rovnice rovín:

Ako rozumieť tejto rovnici? Premýšľajte o tom: „Z“ sa VŽDY rovná nule pre akékoľvek hodnoty „X“ a „Y“. Toto je rovnica "natívnej" súradnicovej roviny. Formálne možno rovnicu prepísať takto: , odkiaľ jasne vidíte, že je nám jedno, aké hodnoty „x“ a „y“ majú, je dôležité, aby sa „z“ rovnalo nule.

Podobne:
– rovnica súradnicovej roviny;
– rovnica súradnicovej roviny.

Trochu si problém skomplikujeme, uvažujme rovinu (tu a ďalej v odseku predpokladáme, že číselné koeficienty sa nerovnajú nule). Prepíšme rovnicu v tvare: . Ako tomu rozumieť? „X“ sa pre akékoľvek hodnoty „y“ a „z“ VŽDY rovná určitému číslu. Táto rovina je rovnobežná s rovinou súradníc. Napríklad rovina je rovnobežná s rovinou a prechádza bodom.

Podobne:
– rovnica roviny, ktorá je rovnobežná s rovinou súradníc;
– rovnica roviny, ktorá je rovnobežná s rovinou súradníc.

Pridajme členov: . Rovnicu možno prepísať takto: , to znamená, že „zet“ môže byť čokoľvek. Čo to znamená? „X“ a „Y“ sú spojené vzťahom, ktorý kreslí určitú priamku v rovine (zistíte rovnica priamky v rovine?). Keďže „z“ môže byť ľubovoľné, táto priamka sa „replikuje“ v akejkoľvek výške. Rovnica teda definuje rovinu rovnobežnú so súradnicovou osou

Podobne:
– rovnica roviny, ktorá je rovnobežná so súradnicovou osou;
– rovnica roviny, ktorá je rovnobežná so súradnicovou osou.

Ak sú voľné členy nula, potom budú roviny priamo prechádzať príslušnými osami. Napríklad klasická „priama úmernosť“: . Nakreslite rovnú čiaru v rovine a mentálne ju vynásobte hore a dole (keďže „Z“ je ľubovoľné). Záver: rovina definovaná rovnicou prechádza súradnicovou osou.

Dokončujeme prehľad: rovnica roviny prechádza cez pôvod. Tu je celkom zrejmé, že bod spĺňa túto rovnicu.

A nakoniec prípad znázornený na obrázku: – rovina je priateľská so všetkými súradnicovými osami, pričom vždy „odreže“ trojuholník, ktorý sa môže nachádzať v ktoromkoľvek z ôsmich oktantov.

Lineárne nerovnosti v priestore

Aby ste porozumeli informáciám, musíte sa dobre naštudovať lineárne nerovnosti v rovine, pretože veľa vecí bude podobných. Tento odsek bude mať stručný prehľad s niekoľkými príkladmi, keďže tento materiál je v praxi pomerne zriedkavý.

Ak rovnica definuje rovinu, potom nerovnosti
opýtať sa polovičné medzery. Ak nerovnosť nie je striktná (posledné dve v zozname), tak riešenie nerovnosti okrem polpriestoru zahŕňa aj samotnú rovinu.

Príklad 5

Nájdite jednotkový normálový vektor roviny .

Riešenie: Jednotkový vektor je vektor, ktorého dĺžka je jedna. Označme tento vektor . Je úplne jasné, že vektory sú kolineárne:

Najprv odstránime normálový vektor z rovnice roviny: .

Ako nájsť jednotkový vektor? Aby ste našli jednotkový vektor, potrebujete každý vydeľte súradnicu vektora dĺžkou vektora.

Prepíšme normálny vektor do formulára a nájdime jeho dĺžku:

Podľa vyššie uvedeného:

Odpoveď:

Overenie: čo bolo potrebné overiť.

Čitatelia, ktorí si pozorne preštudovali posledný odsek lekcie, si to pravdepodobne všimli súradnice jednotkového vektora sú presne smerové kosínusy vektora:

Poďme si oddýchnuť od aktuálneho problému: keď dostanete ľubovoľný nenulový vektor, a podľa podmienky je potrebné nájsť jej smerové kosínusy (pozri posledné úlohy lekcie Bodový súčin vektorov), potom v skutočnosti nájdete jednotkový vektor kolineárny s týmto. Vlastne dve úlohy v jednej fľaši.

Potreba nájsť jednotkový normálový vektor vzniká v niektorých problémoch matematickej analýzy.

Prišli sme na to, ako vyloviť normálny vektor, teraz odpovedzme na opačnú otázku:

Ako vytvoriť rovnicu roviny pomocou bodu a normálového vektora?

Táto tuhá konštrukcia normálneho vektora a bodu je terčom dobre známa. Natiahnite ruku dopredu a v duchu vyberte ľubovoľný bod v priestore, napríklad malú mačku v príborníku. Je zrejmé, že cez tento bod môžete nakresliť jednu rovinu kolmú na vašu ruku.

Rovnica roviny prechádzajúcej bodom kolmým na vektor je vyjadrená vzorcom:

V tejto lekcii sa pozrieme na to, ako použiť determinant na vytvorenie rovinná rovnica. Ak neviete, čo je determinant, prejdite na prvú časť lekcie - „Matice a determinanty“. V opačnom prípade riskujete, že v dnešnom materiáli ničomu nerozumiete.

Rovnica roviny pomocou troch bodov

Prečo vôbec potrebujeme rovinnú rovnicu? Je to jednoduché: ak to poznáme, môžeme ľahko vypočítať uhly, vzdialenosti a iné svinstvá v úlohe C2. Vo všeobecnosti sa bez tejto rovnice nezaobídete. Preto problém formulujeme:

Úloha. V priestore sú uvedené tri body, ktoré neležia na tej istej priamke. Ich súradnice:

M = (x 1, y 1, z 1);
N = (x2, y2, z2);
K = (x3,y3,z3);

Musíte vytvoriť rovnicu pre rovinu prechádzajúcu týmito tromi bodmi. Okrem toho by rovnica mala vyzerať takto:

Ax + By + Cz + D = 0

kde čísla A, B, C a D sú koeficienty, ktoré je v skutočnosti potrebné nájsť.

Ako získať rovnicu roviny, ak sú známe iba súradnice bodov? Najjednoduchší spôsob je dosadiť súradnice do rovnice Ax + By + Cz + D = 0. Získate systém troch rovníc, ktoré sa dajú ľahko vyriešiť.

Mnoho študentov považuje toto riešenie za mimoriadne zdĺhavé a nespoľahlivé. Minuloročná Jednotná štátna skúška z matematiky ukázala, že pravdepodobnosť, že urobíte chybu vo výpočte, je naozaj vysoká.

Najpokročilejší učitelia preto začali hľadať jednoduchšie a elegantnejšie riešenia. A našli to! Pravda, získaná technika sa týka skôr vyššej matematiky. Osobne som sa musel prehrabať celým federálnym zoznamom učebníc, aby som sa uistil, že máme právo používať túto techniku ​​bez akéhokoľvek zdôvodnenia a dôkazov.

Rovnica roviny cez determinant

Dosť bolo textov, poďme na vec. Na začiatok veta o tom, ako súvisí determinant matice a rovnica roviny.

Veta. Nech sú dané súradnice troch bodov, cez ktoré treba nakresliť rovinu: M = (x 1, y 1, z 1); N = (x2, y2, z2); K = (x 3, y3, z 3). Potom možno rovnicu tejto roviny zapísať cez determinant:

Ako príklad skúsme nájsť dvojicu rovín, ktoré sa skutočne vyskytujú v úlohách C2. Pozrite sa, ako rýchlo sa všetko vypočíta:

Ai = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);

Zložíme determinant a prirovnáme ho k nule:

Rozšírime determinant:

a = 1 1 (z − 1) + 0 0 x + (−1) 1 y = z − 1 − y;
b = (−1) 1 x + 0 1 (z − 1) + 10 y = −x;
d = a − b = z − 1 − y − (−x ) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Ako vidíte, pri výpočte čísla d som rovnicu trochu „učesal“, aby premenné x, y a z boli v správnom poradí. To je všetko! Rovnica roviny je pripravená!

Úloha. Napíšte rovnicu pre rovinu prechádzajúcu bodmi:

A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);

Okamžite dosadíme súradnice bodov do determinantu:

Opäť rozširujeme determinant:

a = 11 z + 01 x + 10 y = z;
b = 11 x + 00 z + 11 y = x + y;
d = a − b = z − (x + y ) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

Takže rovnica roviny je opäť získaná! Opäť sme v poslednom kroku museli zmeniť znaky v ňom, aby sme získali „krásnejší“ vzorec. V tomto riešení to nie je vôbec potrebné, ale aj tak sa to odporúča - zjednodušiť ďalšie riešenie problému.

Ako vidíte, skladanie rovnice roviny je teraz oveľa jednoduchšie. Dosadíme body do matice, vypočítame determinant - a je to, rovnica je pripravená.

Tým by sa lekcia mohla skončiť. Mnoho študentov však neustále zabúda, čo je vo vnútri determinantu. Napríklad, ktorý riadok obsahuje x 2 alebo x 3 a ktorý riadok obsahuje iba x. Aby sme to naozaj prehnali, pozrime sa, odkiaľ každé číslo pochádza.

Odkiaľ pochádza vzorec s determinantom?

Poďme teda zistiť, odkiaľ pochádza taká drsná rovnica s determinantom. To vám pomôže zapamätať si ho a úspešne ho aplikovať.

Všetky roviny, ktoré sa objavia v úlohe C2, sú definované tromi bodmi. Tieto body sú vždy vyznačené na výkrese, prípadne aj naznačené priamo v texte úlohy. V každom prípade, aby sme vytvorili rovnicu, budeme musieť zapísať ich súradnice:

M = (x 1, y 1, z 1);
N = (x2, y2, z2);
K = (x 3, y3, z 3).

Zoberme si ďalší bod na našej rovine s ľubovoľnými súradnicami:

T = (x, y, z)

Vezmite ľubovoľný bod z prvých troch bodov (napríklad bod M) a nakreslite z neho vektory do každého z troch zostávajúcich bodov. Dostaneme tri vektory:

MN = (x2 - x1, y2 - y1, z2 - zi);
MK = (x 3 − x 1, y 3 − y 1, z 3 − z 1 );
MT = (x − x 1 , y − y 1 , z − z 1 ).

Teraz z týchto vektorov poskladáme štvorcovú maticu a jej determinant prirovnáme k nule. Súradnice vektorov sa stanú riadkami matice - a dostaneme samotný determinant, ktorý je uvedený vo vete:

Tento vzorec znamená, že objem kvádra postaveného na vektoroch MN, MK a MT je rovný nule. Preto všetky tri vektory ležia v rovnakej rovine. Najmä ľubovoľný bod T = (x, y, z) je presne to, čo sme hľadali.

Nahradenie bodov a čiar determinantu

Determinanty majú niekoľko skvelých vlastností, vďaka ktorým je to ešte jednoduchšie riešenie problému C2. Napríklad nám nezáleží na tom, z ktorého bodu kreslíme vektory. Preto nasledujúce determinanty dávajú rovnakú rovinnú rovnicu ako vyššie:

Môžete tiež vymeniť riadky determinantu. Rovnica zostane nezmenená. Mnohí ľudia napríklad radi píšu čiaru so súradnicami bodu T = (x; y; z) úplne hore. Prosím, ak je to pre vás výhodné:

Niekoho mätie, že jedna z čiar obsahuje premenné x, y a z, ktoré pri dosadzovaní bodov nezmiznú. Ale nemali by zmiznúť! Nahradením čísel do determinantu by ste mali dostať túto konštrukciu:

Potom sa determinant rozšíri podľa diagramu uvedeného na začiatku lekcie a získa sa štandardná rovnica roviny:

Ax + By + Cz + D = 0

Pozrite si príklad. Je to posledná v dnešnej lekcii. Zámerne vymením čiary, aby som sa uistil, že odpoveď poskytne rovnakú rovnicu roviny.

Úloha. Napíšte rovnicu pre rovinu prechádzajúcu bodmi:

B1 = (1, 0, 1);
C = (1,1,0);
D1 = (0, 1, 1).

Takže zvážime 4 body:

B1 = (1, 0, 1);
C = (1,1,0);
D1 = (0, 1, 1);
T = (x, y, z).

Najprv vytvorte štandardný determinant a prirovnajte ho k nule:

Rozšírime determinant:

a = 01 (z - 1) + 10 (x - 1) + (-1) (-1) y = 0 + 0 + y;
b = (−1) 1 (x − 1) + 1 (−1) (z − 1) + 0 0 y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z ) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;

To je všetko, dostali sme odpoveď: x + y + z − 2 = 0.

Teraz preusporiadame pár riadkov v determinante a uvidíme, čo sa stane. Napríklad napíšme riadok s premennými x, y, z nie dole, ale hore:

Výsledný determinant opäť rozšírime:

a = (x − 1) 1 (−1) + (z − 1) (−1) 1 + y 0 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) 10 + y (−1) (−1) + (x − 1) 10 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

Dostali sme presne rovnakú rovinnú rovnicu: x + y + z − 2 = 0. To znamená, že naozaj nezáleží na poradí riadkov. Zostáva už len zapísať odpoveď.

Sme teda presvedčení, že rovnica roviny nezávisí od postupnosti priamok. Môžeme vykonať podobné výpočty a dokázať, že rovnica roviny nezávisí od bodu, ktorého súradnice odčítame od iných bodov.

Vo vyššie uvedenom probléme sme použili bod B 1 = (1, 0, 1), ale bolo celkom možné vziať C = (1, 1, 0) alebo D 1 = (0, 1, 1). Vo všeobecnosti akýkoľvek bod so známymi súradnicami ležiaci v požadovanej rovine.

Aby mohla byť jedna rovina vedená cez ľubovoľné tri body v priestore, je potrebné, aby tieto body neležali na rovnakej priamke.

Uvažujme body M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) vo všeobecnom karteziánskom súradnicovom systéme.

Aby ľubovoľný bod M(x, y, z) ležal v rovnakej rovine s bodmi M 1, M 2, M 3, je potrebné, aby vektory boli koplanárne.

(
) = 0

teda

Rovnica roviny prechádzajúcej tromi bodmi:

Rovnica roviny zadanej dvoma bodmi a vektorom kolineárnym s rovinou.

Nech sú dané body M 1 (x 1,y 1,z 1),M 2 (x 2,y 2,z 2) a vektor
.

Vytvorme rovnicu pre rovinu prechádzajúcu danými bodmi M 1 a M 2 a ľubovoľným bodom M (x, y, z) rovnobežným s vektorom. .

vektory
a vektor
musia byť koplanárne, t.j.

(
) = 0

Rovinná rovnica:

Rovnica roviny pomocou jedného bodu a dvoch vektorov,

kolineárne s rovinou.

Nech sú dané dva vektory
A
, kolineárne roviny. Potom pre ľubovoľný bod M(x, y, z) patriaci rovine, vektory
musí byť koplanárna.

Rovinná rovnica:

Rovnica roviny bodom a normálovým vektorom .

Veta. Ak je bod M daný v priestore 0 (X 0 , r 0 , z 0 ), potom rovnica roviny prechádzajúcej bodom M 0 kolmo na normálny vektor (A, B, C) má tvar:

A(X – X 0 ) + B(r – r 0 ) + C(z – z 0 ) = 0.

Dôkaz. Pre ľubovoľný bod M(x, y, z) patriaci rovine zostavíme vektor. Pretože vektor je normálový vektor, potom je kolmý na rovinu, a teda kolmý na vektor
. Potom skalárny súčin

= 0

Tak dostaneme rovnicu roviny

Veta bola dokázaná.

Rovnica roviny v segmentoch.

Ak vo všeobecnej rovnici Ax + By + Cz + D = 0 delíme obe strany (-D)

,

nahradenie
, dostaneme rovnicu roviny v segmentoch:

Čísla a, b, c sú priesečníky roviny s osami x, y, z.

Rovnica roviny vo vektorovom tvare.

Kde

- vektor polomeru aktuálneho bodu M(x, y, z),

Jednotkový vektor v smere kolmice spadnutej na rovinu z počiatku.

,  a  sú uhly, ktoré zviera tento vektor s osami x, y, z.

p je dĺžka tejto kolmice.

V súradniciach táto rovnica vyzerá takto:

xcos + ycos + zcos - p = 0.

Vzdialenosť od bodu k rovine.

Vzdialenosť od ľubovoľného bodu M 0 (x 0, y 0, z 0) k rovine Ax+By+Cz+D=0 je:

Príklad. Nájdite rovnicu roviny s vedomím, že bod P(4; -3; 12) je základňou kolmice spadnutej z počiatku na túto rovinu.

Takže A = 4/13; B = -3/13; C = 12/13, použijeme vzorec:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Príklad. Nájdite rovnicu roviny prechádzajúcej dvoma bodmi P(2; 0; -1) a

Q(1; -1; 3) kolmá na rovinu 3x + 2y – z + 5 = 0.

Normálny vektor k rovine 3x + 2y – z + 5 = 0
rovnobežne s požadovanou rovinou.

Dostaneme:

Príklad. Nájdite rovnicu roviny prechádzajúcej bodmi A(2, -1, 4) a

B(3, 2, -1) kolmo na rovinu X + pri + 2z – 3 = 0.

Požadovaná rovnica roviny má tvar: A X+B r+C z+ D = 0, normálový vektor k tejto rovine (A, B, C). Vektor
(1, 3, -5) patrí do roviny. Rovina, ktorá je nám daná, kolmá na požadovanú, má normálny vektor (1, 1, 2). Pretože body A a B patria obom rovinám a roviny sú teda navzájom kolmé

Takže normálny vektor (11, -7, -2). Pretože bod A patrí do želanej roviny, potom jeho súradnice musia spĺňať rovnicu tejto roviny, t.j. 112 + 71 - 24 +D= 0;D= -21.

Celkovo dostaneme rovnicu roviny: 11 X - 7r – 2z – 21 = 0.

Príklad. Nájdite rovnicu roviny s vedomím, že bod P(4, -3, 12) je základňou kolmice spadnutej z počiatku do tejto roviny.

Nájdenie súradníc normálového vektora
= (4, -3, 12). Požadovaná rovnica roviny má tvar: 4 X – 3r + 12z+ D = 0. Aby sme našli koeficient D, dosadíme súradnice bodu P do rovnice:

16 + 9 + 144 + D = 0

Celkovo dostaneme požadovanú rovnicu: 4 X – 3r + 12z – 169 = 0

Príklad. Uvedené sú súradnice vrcholov pyramídy A 1 (1; 0; 3), A 2 (2; -1; 3), A 3 (2; 1; 1),

Nájdite dĺžku hrany A 1 A 2.

Nájdite uhol medzi hranami A 1 A 2 a A 1 A 4.

Nájdite uhol medzi hranou A 1 A 4 a plochou A 1 A 2 A 3.

Najprv nájdeme normálový vektor k ploche A 1 A 2 A 3 ako krížový produkt vektorov
A
.

= (2-1; 1-0; 1-3) = (1; 1; -2);

Nájdite uhol medzi normálovým vektorom a vektorom
.

-4 – 4 = -8.

Požadovaný uhol  medzi vektorom a rovinou bude rovný  = 90 0 - .

Nájdite oblasť tváre A 1 A 2 A 3.

Nájdite objem pyramídy.

Nájdite rovnicu roviny A 1 A 2 A 3.

Použime vzorec pre rovnicu roviny prechádzajúcej tromi bodmi.

2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0;

Pri použití počítačovej verzie „ Vyšší kurz matematiky” môžete spustiť program, ktorý vyrieši vyššie uvedený príklad pre ľubovoľné súradnice vrcholov pyramídy.

Ak chcete spustiť program, dvakrát kliknite na ikonu:

V okne programu, ktoré sa otvorí, zadajte súradnice vrcholov pyramídy a stlačte Enter. Týmto spôsobom je možné získať všetky rozhodovacie body jeden po druhom.

Poznámka: Na spustenie programu musíte mať na svojom počítači nainštalovaný program Maple ( Waterloo Maple Inc.), akúkoľvek verziu začínajúcu MapleV Release 4.