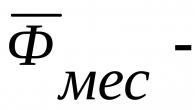Vous savez bien que selon la forme de la trajectoire, le mouvement se décompose en rectiligne Et curviligne. Nous avons appris à travailler avec le mouvement rectiligne dans les leçons précédentes, à savoir résoudre le principal problème de mécanique pour ce type de mouvement.

Cependant, il est clair que dans le monde réel, nous avons le plus souvent affaire à un mouvement curviligne, lorsque la trajectoire est une ligne courbe. Des exemples d'un tel mouvement sont la trajectoire d'un corps projeté en biais par rapport à l'horizon, le mouvement de la Terre autour du Soleil et même la trajectoire du mouvement de vos yeux, qui suivent maintenant cette note.

Cette leçon sera consacrée à la question de savoir comment le principal problème de mécanique est résolu dans le cas d'un mouvement curviligne.

Pour commencer, déterminons quelles différences fondamentales existent entre le mouvement curviligne (Fig. 1) par rapport au mouvement rectiligne et à quoi conduisent ces différences.

Riz. 1. Trajectoire du mouvement curviligne

Parlons de la façon dont il est pratique de décrire le mouvement d'un corps lors d'un mouvement curviligne.

Le mouvement peut être divisé en sections distinctes, dans chacune desquelles le mouvement peut être considéré comme rectiligne (Fig. 2).

Riz. 2. Diviser le mouvement curviligne en sections de mouvement rectiligne

Toutefois, l’approche suivante est plus pratique. Nous imaginerons ce mouvement comme une combinaison de plusieurs mouvements selon des arcs de cercle (Fig. 3). Veuillez noter qu'il y a moins de cloisons de ce type que dans le cas précédent, de plus, le mouvement le long du cercle est curviligne. De plus, les exemples de mouvements en cercle sont très courants dans la nature. De ceci nous pouvons conclure :

Afin de décrire un mouvement curviligne, vous devez apprendre à décrire un mouvement dans un cercle, puis représenter un mouvement arbitraire sous la forme d'ensembles de mouvements le long d'arcs de cercle.

Riz. 3. Partitionner le mouvement curviligne en mouvement le long d'arcs de cercle

Commençons donc l’étude du mouvement curviligne par l’étude du mouvement uniforme dans un cercle. Voyons quelles sont les différences fondamentales entre le mouvement curviligne et le mouvement rectiligne. Pour commencer, rappelons qu'en neuvième année nous avons étudié le fait que la vitesse d'un corps lorsqu'il se déplace en cercle est dirigée de manière tangente à la trajectoire (Fig. 4). À propos, vous pouvez observer ce fait expérimentalement si vous observez le mouvement des étincelles lors de l'utilisation d'une pierre à aiguiser.

Considérons le mouvement d'un corps le long d'un arc de cercle (Fig. 5).

Riz. 5. Vitesse d'un corps lors d'un déplacement en cercle

Veuillez noter que dans ce cas le module de la vitesse du corps en un point est égal au module de la vitesse du corps en ce point :

Cependant, un vecteur n’est pas égal à un vecteur. Nous avons donc un vecteur de différence de vitesse (Fig. 6) :

Riz. 6. Vecteur de différence de vitesse

De plus, le changement de vitesse s'est produit après un certain temps. On obtient donc la combinaison familière :

Ce n'est rien de plus qu'un changement de vitesse sur une période de temps ou une accélération d'un corps. Une conclusion très importante peut être tirée :

Le mouvement le long d’une trajectoire courbe est accéléré. La nature de cette accélération est un changement continu de la direction du vecteur vitesse.

Notons encore une fois que, même si l’on dit que le corps se déplace uniformément en cercle, cela signifie que le module de la vitesse du corps ne change pas. Cependant, un tel mouvement est toujours accéléré, puisque la direction de la vitesse change.

En neuvième année, vous avez étudié à quoi correspond cette accélération et comment elle est dirigée (Fig. 7). L'accélération centripète est toujours dirigée vers le centre du cercle le long duquel le corps se déplace.

Riz. 7. Accélération centripète

Le module d'accélération centripète peut être calculé par la formule :

Passons à la description du mouvement uniforme d'un corps dans un cercle. Admettons que la vitesse que vous avez utilisée pour décrire le mouvement de translation sera désormais appelée vitesse linéaire. Et par vitesse linéaire on entendra la vitesse instantanée au point de la trajectoire d'un corps en rotation.

Riz. 8. Mouvement des points du disque

Considérons un disque qui tourne dans le sens des aiguilles d’une montre pour plus de précision. Sur son rayon nous marquons deux points et (Fig. 8). Considérons leur mouvement. Au fil du temps, ces points se déplaceront le long des arcs de cercle et deviendront des points et. Il est évident que la pointe a bougé plus que la pointe. De là, nous pouvons conclure que plus un point est éloigné de l’axe de rotation, plus la vitesse linéaire à laquelle il se déplace est grande.

Cependant, si l'on regarde attentivement les points et , on peut dire que l'angle dont ils ont tourné par rapport à l'axe de rotation est resté inchangé. Ce sont les caractéristiques angulaires que nous utiliserons pour décrire le mouvement en cercle. Notez que pour décrire un mouvement circulaire, nous pouvons utiliser coin caractéristiques.

Commençons par considérer le mouvement dans un cercle avec le cas le plus simple : un mouvement uniforme dans un cercle. Rappelons que le mouvement de translation uniforme est un mouvement dans lequel le corps effectue des mouvements égaux sur des périodes de temps égales. Par analogie, on peut donner la définition du mouvement uniforme dans un cercle.

Un mouvement circulaire uniforme est un mouvement dans lequel le corps tourne selon des angles égaux sur des intervalles de temps égaux.

Semblable au concept de vitesse linéaire, le concept de vitesse angulaire est introduit.

Vitesse angulaire d'un mouvement uniforme ( est une grandeur physique égale au rapport de l'angle selon lequel le corps a tourné au temps pendant lequel cette rotation s'est produite.

En physique, la mesure d'angle radian est le plus souvent utilisée. Par exemple, l'angle b est égal aux radians. La vitesse angulaire est mesurée en radians par seconde :

Trouvons le lien entre la vitesse angulaire de rotation d'un point et la vitesse linéaire de ce point.

Riz. 9. Relation entre vitesse angulaire et vitesse linéaire

Lors de la rotation, un point passe un arc de longueur , tournant selon un angle . A partir de la définition de la mesure radian d’un angle on peut écrire :

Divisons les côtés gauche et droit de l'égalité par la période de temps pendant laquelle le mouvement a été effectué, puis utilisons la définition des vitesses angulaires et linéaires :

Attention, plus un point est éloigné de l’axe de rotation, plus sa vitesse linéaire est élevée. Et les points situés sur l'axe de rotation lui-même sont immobiles. Un exemple en est un carrousel : plus vous êtes proche du centre du carrousel, plus il vous est facile d'y rester.

Cette dépendance des vitesses linéaires et angulaires est utilisée dans les satellites géostationnaires (satellites toujours situés au-dessus du même point de la surface de la Terre). Grâce à ces satellites, nous pouvons recevoir des signaux de télévision.

Rappelons que nous avons introduit plus haut les notions de période et de fréquence de rotation.

La période de rotation est la durée d'un tour complet. La période de rotation est indiquée par une lettre et mesurée en secondes SI :

La fréquence de rotation est une grandeur physique égale au nombre de tours qu'un corps effectue par unité de temps.

La fréquence est indiquée par une lettre et mesurée en secondes réciproques :

Ils sont liés par la relation :

Il existe une relation entre la vitesse angulaire et la fréquence de rotation du corps. Si l’on se souvient qu’un tour complet est égal à , il est facile de voir que la vitesse angulaire est :

En substituant ces expressions dans la relation entre vitesse angulaire et vitesse linéaire, nous pouvons obtenir la dépendance de la vitesse linéaire sur la période ou la fréquence :

Écrivons également la relation entre l'accélération centripète et ces quantités :

Ainsi, nous connaissons la relation entre toutes les caractéristiques du mouvement circulaire uniforme.

Résumons. Dans cette leçon, nous avons commencé à décrire le mouvement curviligne. Nous avons compris comment relier le mouvement curviligne au mouvement circulaire. Le mouvement circulaire est toujours accéléré et la présence d'une accélération détermine le fait que la vitesse change toujours de direction. Cette accélération est dite centripète. Enfin, nous avons rappelé certaines caractéristiques du mouvement circulaire (vitesse linéaire, vitesse angulaire, période et fréquence de rotation) et trouvé les relations entre elles.

Bibliographie

1. G.Ya. Myakishev, B.B. Boukhovtsev, N.N. Sotski. Physique 10. - M. : Éducation, 2008.
2. A.P. Rymkevitch. La physique. Livre de problèmes 10-11. - M. : Outarde, 2006.
3. O.Ya. Savtchenko. Problèmes de physique. - M. : Nauka, 1988.
4. UN V. Perychkine, V.V. Krauklis. Cours de physique. T. 1. - M. : Etat. professeur éd. min. éducation de la RSFSR, 1957.

1. Аyp.ru ().
2. Wikipédia ().

Devoirs

Après avoir résolu les problèmes de cette leçon, vous pourrez vous préparer aux questions 1 de l'examen d'État et aux questions A1, A2 de l'examen d'État unifié.

1. Problèmes 92, 94, 98, 106, 110 - Sam. problèmes A.P. Rymkevitch, éd. dix
2. Calculez la vitesse angulaire des aiguilles des minutes, des secondes et des heures de l'horloge. Calculez l'accélération centripète agissant sur les pointes de ces flèches si le rayon de chacune d'elles est d'un mètre.

Lors d'un mouvement curviligne, la direction du vecteur vitesse change. Dans le même temps, son module, c'est-à-dire sa longueur, peut également changer. Dans ce cas, le vecteur accélération se décompose en deux composantes : tangente à la trajectoire et perpendiculaire à la trajectoire (Fig. 10). Le composant s'appelle tangentiel accélération (tangentielle), composante – normale(accélération centripète.

Accélération lors d'un mouvement courbe

L'accélération tangentielle caractérise le taux de changement de vitesse linéaire et l'accélération normale caractérise le taux de changement de direction du mouvement.

L'accélération totale est égale à la somme vectorielle des accélérations tangentielle et normale :

(15)

Le module d'accélération total est égal à :

.

Considérons le mouvement uniforme d'un point autour d'un cercle. Où Et . Supposons qu'à l'instant t considéré, le point soit en position 1 (Fig. 11). Après le temps Δt, le point sera en position 2, après avoir parcouru le chemin Δs, égal à l'arc 1-2. Dans ce cas, la vitesse du point v augmente Δv, à la suite de quoi le vecteur vitesse, restant inchangé en amplitude, tournera d'un angle Δφ , coïncidant en taille avec l'angle central basé sur un arc de longueur Δs:

(16)

où R est le rayon du cercle le long duquel le point se déplace. Trouvons l'incrément du vecteur vitesse. Pour ce faire, déplaçons le vecteur. de sorte que son début coïncide avec le début du vecteur. Ensuite le vecteur sera représenté par un segment tracé de la fin du vecteur à la fin du vecteur . Ce segment sert de base à un triangle isocèle avec des côtés et et l'angle Δφ au sommet. Si l'angle Δφ est petit (ce qui est vrai pour Δt petit), pour les côtés de ce triangle on peut écrire approximativement :

.

En substituant ici Δφ de (16), nous obtenons une expression pour le module du vecteur :

.

En divisant les deux côtés de l'équation par Δt et en passant à la limite, on obtient la valeur de l'accélération centripète :

Voici les quantités v Et R. sont constants, ils peuvent donc être portés au-delà du signe limite. La limite du rapport est le module de vitesse On l'appelle aussi vitesse linéaire.

Rayon de courbure

Le rayon du cercle R s'appelle rayon de courbure trajectoires. L’inverse de R est appelé courbure de la trajectoire :

.

où R est le rayon du cercle en question. Si α est l'angle au centre correspondant à l'arc de cercle s, alors, comme on le sait, la relation entre R, α et s est vraie :

s = Ra. (18)

La notion de rayon de courbure s'applique non seulement à un cercle, mais aussi à toute ligne courbe. Le rayon de courbure (ou sa valeur inverse - courbure) caractérise le degré de courbure de la ligne. Plus le rayon de courbure est petit (respectivement plus la courbure est grande), plus la ligne est fortement courbée. Examinons ce concept plus en détail.

Le cercle de courbure d'une ligne plate en un certain point A est la position limite d'un cercle passant par le point A et deux autres points B 1 et B 2 lorsqu'ils s'approchent du point A à l'infini (sur la figure 12, la courbe est tracée par un ligne continue, et le cercle de courbure par une ligne pointillée). Le rayon du cercle de courbure donne le rayon de courbure de la courbe considérée au point A, et le centre de ce cercle donne le centre de courbure de la courbe pour ce même point A.

Aux points B 1 et B 2, tracez les tangentes B 1 D et B 2 E à un cercle passant par les points B 1, A et B 2. Les normales à ces tangentes B 1 C et B 2 C représenteront les rayons R du cercle et se couperont en son centre C. Introduisons l'angle Δα entre les normales B1 C et B 2 C ; évidemment, il est égal à l'angle entre les tangentes B 1 D et B 2 E. Notons la section de la courbe entre les points B 1 et B 2 par Δs. Puis selon la formule (18) :

.

Cercle de courbure d'une ligne courbe plate

Détermination de la courbure d'une courbe plane en différents points

En figue. 13 montre des cercles de courbure d'une ligne plate en différents points. Au point A 1, où la courbe est plus plate, le rayon de courbure est plus grand qu'au point A 2, respectivement, la courbure de la ligne au point A 1 sera inférieure à celle du point A 2. Au point A 3, la courbe est encore plus plate qu'aux points A 1 et A 2, donc le rayon de courbure en ce point sera plus grand et la courbure moindre. De plus, le cercle de courbure au point A3 se situe de l'autre côté de la courbe. Par conséquent, la valeur de courbure en ce point se voit attribuer un signe opposé au signe de courbure aux points A 1 et A 2 : si la courbure aux points A 1 et A 2 est considérée comme positive, alors la courbure au point A 3 sera négatif.

Nous savons que tout mouvement curviligne se produit sous l’influence d’une force dirigée selon un angle par rapport à la vitesse. Dans le cas d'un mouvement uniforme autour d'un cercle, cet angle sera droit. En fait, si, par exemple, vous faites tourner une balle attachée à une corde, alors la direction de la vitesse de la balle à tout moment est perpendiculaire à la corde.

La force de tension de la corde, qui maintient la balle sur le cercle, est dirigée le long de la corde vers le centre de rotation.

Selon la deuxième loi de Newton, cette force fera accélérer le corps dans la même direction. L'accélération dirigée radialement vers le centre de rotation est appelée accélération centripète .

Dérivons une formule pour déterminer l'ampleur de l'accélération centripète.

Tout d’abord, sachez que le mouvement circulaire est un mouvement complexe. Sous l'influence de la force centripète, le corps se déplace vers le centre de rotation et en même temps, par inertie, s'éloigne de ce centre tangentiellement au cercle.

Supposons que pendant le temps t un corps, se déplaçant uniformément avec une vitesse v, se soit déplacé de D à E. Supposons qu'au moment où le corps était au point D, la force centripète cesserait d'agir sur lui. Puis au temps t il se déplacerait vers le point K situé sur la tangente DL. Si au moment initial le corps était sous l'influence d'une seule force centripète (ne se déplaçant pas par inertie), alors au temps t, se déplaçant uniformément accéléré, il se déplacerait vers le point F situé sur la droite DC. De l'addition de ces deux mouvements au cours du temps t, on obtient le mouvement résultant le long de l'arc DE.

Force centripète

La force qui maintient un corps en rotation sur un cercle et est dirigée vers le centre de rotation est appelée force centripète .

Pour obtenir une formule permettant de calculer l’ampleur de la force centripète, vous devez utiliser la deuxième loi de Newton, qui s’applique à tout mouvement curviligne.

En substituant la valeur de l'accélération centripète a = v 2 / R dans la formule F = ma, nous obtenons la formule de la force centripète :

F = mv2 / R

L'ampleur de la force centripète est égale au produit de la masse du corps par le carré de la vitesse linéaire divisé par le rayon..

Si la vitesse angulaire du corps est donnée, alors il est plus pratique de calculer la force centripète en utilisant la formule : F = m ? 2R, où ? 2 R – accélération centripète.

De la première formule, il ressort clairement qu'à vitesse égale, plus le rayon du cercle est petit, plus la force centripète est grande. Ainsi, lors des virages sur route, un corps en mouvement (train, voiture, vélo) doit agir vers le centre de la courbe, plus la force est grande, plus le virage est serré, c'est-à-dire plus le rayon de la courbe est petit.

La force centripète dépend de la vitesse linéaire : à mesure que la vitesse augmente, elle augmente. Tous les patineurs, skieurs et cyclistes le savent bien : plus on avance vite, plus il est difficile d'effectuer un virage. Les conducteurs savent très bien à quel point il est dangereux de faire tourner brusquement une voiture à grande vitesse.

Vitesse linéaire

Mécanismes centrifuges

Mouvement d'un corps projeté incliné par rapport à l'horizontale

Jetons un corps en biais par rapport à l'horizon. En observant son mouvement, nous remarquerons que le corps s'élève d'abord en se déplaçant le long d'une courbe, puis retombe également le long d'une courbe.

Si vous dirigez un jet d'eau sous différents angles par rapport à l'horizon, vous pouvez voir qu'au début, à mesure que l'angle augmente, le jet frappe de plus en plus loin. À un angle de 45° par rapport à l'horizon (si l'on ne tient pas compte de la résistance de l'air), la portée est la plus grande. À mesure que l’angle augmente, la portée diminue.

Pour construire la trajectoire d'un corps projeté selon un angle par rapport à l'horizon, on trace une droite horizontale OA et on lui trace une droite OS selon un angle donné.

Sur la ligne OS à l'échelle sélectionnée, nous disposons des segments numériquement égaux aux chemins parcourus dans la direction du lancer (0-1, 1-2, 2-3, 3-4). À partir des points 1, 2, 3, etc., nous abaissons les perpendiculaires à OA et y disposons des segments numériquement égaux aux chemins parcourus par un corps en chute libre pendant 1 seconde (1-I), 2 secondes (2-II ), 3 sec (3-III), etc. Nous connectons les points 0, I, II, III, IV, etc. avec une courbe lisse.

La trajectoire du corps est symétrique par rapport à la ligne verticale passant par le point IV.

La résistance de l'air réduit à la fois la portée de vol et l'altitude maximale de vol, et la trajectoire devient asymétrique. Ce sont par exemple les trajectoires des obus et des balles. Sur la figure, la courbe pleine montre schématiquement la trajectoire d'un projectile dans les airs, et la courbe en pointillés la montre dans un espace sans air. L’exemple suivant montre à quel point la résistance de l’air modifie la plage de vol. En l'absence de résistance aérienne, un obus de canon de 76 mm tiré à un angle de 20° par rapport à l'horizon parcourrait 24 km. Dans les airs, ce projectile parcourt environ 7 km.

Troisième loi de Newton

Mouvement d'un corps projeté horizontalement

Indépendance des mouvements

Tout mouvement curviligne est un mouvement complexe constitué d'un mouvement par inertie et d'un mouvement sous l'influence d'une force dirigée selon un angle par rapport à la vitesse du corps. Cela peut être montré dans l’exemple suivant.

Supposons que la balle se déplace le long de la table de manière uniforme et en ligne droite. Lorsque la balle sort de la table, son poids n'est plus équilibré par la force de pression de la table et, par inertie, en maintenant un mouvement uniforme et linéaire, elle commence simultanément à tomber. Grâce à l'addition de mouvements - rectilignes uniformes par inertie et uniformément accélérés sous l'influence de la gravité - la balle se déplace le long d'une ligne courbe.

On peut montrer expérimentalement que ces mouvements sont indépendants les uns des autres.

La figure montre un ressort qui, se pliant sous le coup d'un marteau, peut mettre l'une des billes en mouvement dans une direction horizontale et en même temps libérer l'autre bille, de sorte que les deux commencent à bouger en même temps. : le premier selon une courbe, le second selon une verticale descendante. Les deux balles toucheront le sol en même temps ; par conséquent, le temps de chute des deux balles est le même. De là, nous pouvons conclure que le mouvement de la balle sous l'influence de la gravité ne dépend pas du fait que la balle était au repos au moment initial ou qu'elle se déplaçait dans la direction horizontale.

Cette expérience illustre un point très important en mécanique, appelé principe d'indépendance des mouvements.

Mouvement uniforme autour d'un cercle

L’un des types de mouvement curviligne les plus simples et les plus courants est le mouvement uniforme d’un corps en cercle. Par exemple, des parties de volants d’inertie, des points à la surface de la Terre se déplacent le long d’un cercle pendant la rotation quotidienne de la Terre, etc.

Introduisons les grandeurs qui caractérisent ce mouvement. Regardons le dessin. Supposons que lorsqu'un corps tourne, l'un de ses points se déplace de A à B pendant le temps t. Le rayon reliant le point A au centre du cercle tourne d'un angle ? (grec « phi »). La vitesse de rotation d'un point peut-elle être caractérisée par la grandeur du rapport angulaire ? au temps t, c'est-à-dire ? /t.

Vitesse angulaire

Le rapport de l'angle de rotation du rayon reliant le point mobile au centre de rotation à la période de temps pendant laquelle cette rotation se produit est appelé vitesse angulaire.

Désignant la vitesse angulaire avec une lettre grecque ? (« oméga »), vous pouvez écrire :

? = ? /t

La vitesse angulaire est numériquement égale à l'angle de rotation par unité de temps.

Avec un mouvement uniforme dans un cercle, la vitesse angulaire est une quantité constante.

Lors du calcul de la vitesse angulaire, l'angle de rotation est généralement mesuré en radians. Un radian est un angle au centre dont la longueur de l'arc est égale au rayon de cet arc.

Le mouvement des corps sous l'action d'une force dirigée selon un angle par rapport à la vitesse

En considérant le mouvement rectiligne, il est devenu connu que si une force agit sur un corps dans la direction du mouvement, alors le mouvement du corps restera rectiligne. Seule la vitesse changera. De plus, si la direction de la force coïncide avec la direction de la vitesse, le mouvement sera rectiligne et accéléré. Dans le cas d’une force de direction opposée, le mouvement sera droit et lent. Il s’agit par exemple du mouvement d’un corps projeté verticalement vers le bas et du mouvement d’un corps projeté verticalement vers le haut.

Considérons maintenant comment un corps se déplacera sous l'influence d'une force dirigée selon un angle par rapport à la direction de la vitesse.

Regardons d'abord l'expérience. Créons une trajectoire de mouvement d'une bille d'acier à proximité d'un aimant. Nous remarquons immédiatement que loin de l'aimant, la balle s'est déplacée en ligne droite, mais à l'approche de l'aimant, la trajectoire de la balle était pliée et la balle s'est déplacée le long d'une courbe. La direction de sa vitesse changeait constamment. La raison en était l’action de l’aimant sur la balle.

Nous pouvons faire bouger un corps en mouvement rectiligne le long d'une courbe si nous le poussons, si nous tirons un fil qui y est attaché, etc., à condition que la force soit dirigée selon un angle par rapport à la vitesse de mouvement du corps.

Ainsi, le mouvement curviligne d’un corps se produit sous l’action d’une force dirigée selon un angle par rapport à la direction de la vitesse du corps.

Selon la direction et l'ampleur de la force agissant sur le corps, les mouvements curvilignes peuvent être très divers. Les types de mouvements curvilignes les plus simples sont les mouvements en cercle, en parabole et en ellipse.

Exemples d'action de la force centripète

Dans certains cas, la force centripète est la résultante de deux forces agissant sur un corps se déplaçant en cercle.

Examinons quelques exemples de ce type.

1. Une voiture se déplace le long d'un pont concave avec une vitesse v, la masse de la voiture est t et le rayon de courbure du pont est R. Quelle est la force de pression exercée par la voiture sur le pont à son point le plus bas ?

Déterminons d'abord quelles forces agissent sur la voiture. Il existe deux forces de ce type : le poids de la voiture et la force de pression du pont sur la voiture. (Nous excluons de la considération la force de friction dans ce cas et dans tous les gagnants suivants).

Lorsque la voiture est à l’arrêt, ces forces, de même ampleur et dirigées dans des directions opposées, s’équilibrent.

Lorsqu’une voiture se déplace le long d’un pont, comme tout corps se déplaçant en cercle, elle est soumise à l’action d’une force centripète. Quelle est la source de ce pouvoir ? La source de cette force ne peut être que l’action du pont sur la voiture. La force Q avec laquelle le pont appuie sur une voiture en mouvement doit non seulement équilibrer le poids de la voiture P, mais aussi la forcer à se déplacer en cercle, créant la force centripète F nécessaire à cela. La force F ne peut être que la résultante de. les forces P et Q, puisqu'elles sont le résultat de l'interaction entre un véhicule en mouvement et un pont.

Avec l'aide de cette leçon, vous pouvez étudier de manière indépendante le sujet « Mouvement rectiligne et curviligne. Mouvement d'un corps en cercle avec une vitesse absolue constante. Tout d’abord, nous caractériserons les mouvements rectilignes et curvilignes en considérant comment, dans ces types de mouvements, le vecteur vitesse et la force appliquée au corps sont liés. Ensuite, nous considérons un cas particulier où un corps se déplace en cercle avec une vitesse constante en valeur absolue.

Dans la leçon précédente, nous avons abordé les questions liées à la loi de la gravitation universelle. Le sujet de la leçon d'aujourd'hui est étroitement lié à cette loi ; nous nous tournerons vers le mouvement uniforme d'un corps dans un cercle.

Nous avons dit plus tôt que mouvement - Il s'agit d'un changement de position d'un corps dans l'espace par rapport à d'autres corps au fil du temps. Le mouvement et la direction du mouvement sont également caractérisés par la vitesse. Le changement de vitesse et le type de mouvement lui-même sont associés à l'action de la force. Si une force agit sur un corps, alors celui-ci change de vitesse.

Si la force est dirigée parallèlement au mouvement du corps, alors ce mouvement sera direct(Fig. 1).

Riz. 1. Mouvement en ligne droite

Curviligne il y aura un tel mouvement lorsque la vitesse du corps et la force appliquée à ce corps seront dirigées l'une par rapport à l'autre selon un certain angle (Fig. 2). Dans ce cas, la vitesse changera de direction.

Riz. 2. Mouvement curviligne

Donc quand mouvement droit le vecteur vitesse est dirigé dans la même direction que la force appliquée au corps. UN mouvement curviligne Il s'agit d'un tel mouvement lorsque le vecteur vitesse et la force appliquée au corps sont situés à un certain angle l'un par rapport à l'autre.

Considérons un cas particulier de mouvement curviligne, lorsqu'un corps se déplace en cercle avec une vitesse constante en valeur absolue. Lorsqu’un corps se déplace en cercle à vitesse constante, seule la direction de la vitesse change. En valeur absolue, elle reste constante, mais la direction de la vitesse change. Ce changement de vitesse entraîne la présence d'une accélération dans le corps, appelée centripète.

Riz. 6. Mouvement le long d'un chemin courbe

Si la trajectoire du mouvement d’un corps est une courbe, alors elle peut être représentée comme un ensemble de mouvements le long d’arcs de cercle, comme le montre la Fig. 6.

En figue. La figure 7 montre comment la direction du vecteur vitesse change. La vitesse lors d'un tel mouvement est dirigée tangentiellement au cercle le long de l'arc duquel le corps se déplace. Ainsi, sa direction change constamment. Même si la vitesse absolue reste constante, un changement de vitesse entraîne une accélération :

Dans ce cas accélération sera dirigé vers le centre du cercle. C'est pourquoi on l'appelle centripète.

Pourquoi l’accélération centripète est-elle dirigée vers le centre ?

Rappelez-vous que si un corps se déplace le long d’une trajectoire courbe, alors sa vitesse est dirigée tangentiellement. La vitesse est une quantité vectorielle. Un vecteur a une valeur numérique et une direction. La vitesse change continuellement de direction à mesure que le corps bouge. C'est-à-dire que la différence de vitesses à différents moments ne sera pas égale à zéro (), contrairement au mouvement rectiligne uniforme.

Nous avons donc un changement de vitesse sur une certaine période de temps. Le rapport à est l'accélération. Nous arrivons à la conclusion que, même si la vitesse ne change pas en valeur absolue, un corps effectuant un mouvement uniforme en cercle a une accélération.

Où est dirigée cette accélération ? Regardons la fig. 3. Certains corps se déplacent de manière curviligne (le long d’un arc). La vitesse du corps aux points 1 et 2 est dirigée tangentiellement. Le corps se déplace uniformément, c'est-à-dire que les modules de vitesse sont égaux : , mais les directions des vitesses ne coïncident pas.

Riz. 3. Mouvement du corps en cercle

Soustrayez-en la vitesse et obtenez le vecteur. Pour ce faire, vous devez relier les débuts des deux vecteurs. En parallèle, déplacez le vecteur au début du vecteur. Nous construisons un triangle. Le troisième côté du triangle sera le vecteur différence de vitesse (Fig. 4).

Riz. 4. Vecteur de différence de vitesse

Le vecteur est dirigé vers le cercle.

Considérons un triangle formé par les vecteurs vitesse et le vecteur différence (Fig. 5).

Riz. 5. Triangle formé par les vecteurs vitesses

Ce triangle est isocèle (les modules de vitesse sont égaux). Cela signifie que les angles à la base sont égaux. Écrivons l'égalité pour la somme des angles d'un triangle :

Voyons où est dirigée l'accélération en un point donné de la trajectoire. Pour ce faire, nous allons commencer à rapprocher le point 2 du point 1. Avec une telle diligence illimitée, l'angle tendra vers 0 et l'angle tendra vers . L'angle entre le vecteur de changement de vitesse et le vecteur vitesse lui-même est . La vitesse est dirigée tangentiellement et le vecteur de changement de vitesse est dirigé vers le centre du cercle. Cela signifie que l’accélération est également dirigée vers le centre du cercle. C'est pourquoi cette accélération est appelée centripète.

Comment trouver l’accélération centripète ?

Considérons la trajectoire le long de laquelle le corps se déplace. Dans ce cas, il s'agit d'un arc de cercle (Fig. 8).

Riz. 8. Mouvement du corps en cercle

La figure montre deux triangles : un triangle formé par les vitesses et un triangle formé par les rayons et le vecteur de déplacement. Si les points 1 et 2 sont très proches, alors le vecteur déplacement coïncidera avec le vecteur trajectoire. Les deux triangles sont isocèles avec les mêmes angles au sommet. Les triangles sont donc semblables. Cela signifie que les côtés correspondants des triangles sont également liés :

Le déplacement est égal au produit de la vitesse et du temps : . En substituant cette formule, nous pouvons obtenir l'expression suivante pour l'accélération centripète :

Vitesse angulaire désigné par la lettre grecque oméga (ω), il indique l'angle selon lequel le corps tourne par unité de temps (Fig. 9). Il s’agit de l’ampleur de l’arc en degrés parcouru par le corps sur une certaine période de temps.

Riz. 9. Vitesse angulaire

Notons que si un corps rigide tourne, alors la vitesse angulaire de tout point de ce corps sera une valeur constante. Que le point soit situé plus près ou plus loin du centre de rotation n'a pas d'importance, c'est-à-dire qu'il ne dépend pas du rayon.

L'unité de mesure dans ce cas sera soit les degrés par seconde () soit les radians par seconde (). Souvent, le mot « radian » n'est pas écrit, mais simplement écrit. Par exemple, trouvons quelle est la vitesse angulaire de la Terre. La Terre fait une rotation complète en une heure, et dans ce cas on peut dire que la vitesse angulaire est égale à :

Faites également attention à la relation entre les vitesses angulaires et linéaires :

La vitesse linéaire est directement proportionnelle au rayon. Plus le rayon est grand, plus la vitesse linéaire est grande. Ainsi, en nous éloignant du centre de rotation, nous augmentons notre vitesse linéaire.

Il convient de noter que le mouvement circulaire à vitesse constante est un cas particulier de mouvement. Cependant, le mouvement autour du cercle peut être inégal. La vitesse peut changer non seulement de direction et rester la même en ampleur, mais aussi changer de valeur, c'est-à-dire qu'en plus d'un changement de direction, il y a également un changement dans l'ampleur de la vitesse. Dans ce cas, nous parlons du mouvement dit accéléré en cercle.

Qu'est-ce qu'un radian ?

Il existe deux unités pour mesurer les angles : les degrés et les radians. En physique, en règle générale, la mesure d'angle en radian est la principale.

Construisons un angle au centre qui repose sur un arc de longueur .

La cinématique étudie le mouvement sans identifier les causes qui provoquent ce mouvement. La cinématique est une branche de la mécanique. La tâche principale de la cinématique est la détermination mathématique de la position et des caractéristiques du mouvement de points ou de corps dans le temps.

Grandeurs cinématiques de base :

- Se déplacer() - un vecteur reliant les points de début et de fin.

r – rayon vecteur, détermine la position du MT dans l'espace.

- Vitesse– rapport chemin/temps .

- Chemin- l'ensemble des points par lesquels le corps est passé.

- Accélération – le taux de changement de vitesse, c'est-à-dire la dérivée première de la vitesse.

2. Accélération lors d'un mouvement courbe : accélération normale et tangentielle. Rotation à plat. Vitesse angulaire, accélération.

Mouvement curviligne est un mouvement dont la trajectoire est une ligne courbe. Un exemple de mouvement curviligne est le mouvement des planètes, l’extrémité d’une aiguille d’horloge le long d’un cadran, etc.

Mouvement curviligne– c’est toujours un mouvement accéléré. Autrement dit, l'accélération lors d'un mouvement curviligne est toujours présente, même si le module de vitesse ne change pas, mais uniquement la direction de la vitesse.

Changement de vitesse par unité de temps – c'est l'accélération tangentielle:

Où 𝛖 τ , 𝛖 0 sont les valeurs de vitesse au temps t 0 + Δt et t 0, respectivement. Accélération tangentielle en un point donné de la trajectoire, la direction coïncide avec la direction de la vitesse de déplacement du corps ou lui est opposée.

Accélération normale est le changement de vitesse en direction par unité de temps :

Accélération normale dirigé selon le rayon de courbure de la trajectoire (vers l'axe de rotation). L'accélération normale est perpendiculaire à la direction de la vitesse.

Pleine accélération avec un mouvement curviligne du corps uniformément variable, il est égal à :

-vitesse angulaire montre l'angle selon lequel un point tourne pendant un mouvement uniforme dans un cercle par unité de temps. L'unité SI est le rad/s.

Rotation à plat est la rotation de tous les vecteurs vitesse des points du corps dans un plan.

3. Relation entre les vecteurs vitesse et vitesse angulaire d'un point matériel. Accélération normale, tangentielle et complète.

Accélération tangentielle (tangentielle)– c'est la composante du vecteur accélération dirigée le long de la tangente à la trajectoire en un point donné de la trajectoire du mouvement. L'accélération tangentielle caractérise le changement de vitesse modulo lors d'un mouvement curviligne.

Accélération normale (centripète) est la composante du vecteur accélération dirigée le long de la normale à la trajectoire du mouvement en un point donné de la trajectoire du corps. C'est-à-dire que le vecteur d'accélération normal est perpendiculaire à la vitesse linéaire du mouvement (voir Fig. 1.10). L'accélération normale caractérise le changement de vitesse en direction et est désignée par la lettre n. Le vecteur accélération normale est dirigé le long du rayon de courbure de la trajectoire.

Pleine accélération en mouvement curviligne, il se compose d'accélérations tangentielles et normales selon la règle de l'addition vectorielle et est déterminé par la formule.