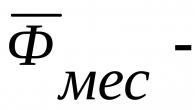Rozwiązywanie prostych równań liniowych. Rozwiązywanie równań liniowych z przykładami Równanie przez 5

zostaw komentarz 6,950

Lekcja nr 33

Temat: Równania

Cele Lekcji:

Podsumuj i usystematyzuj wiedzę uczniów na badany temat, kontynuuj pracę nad rozwijaniem umiejętności rozwiązywania równań i problemów poprzez układanie równań.

Popraw umiejętności obsługi komputera uczniów

Kształtuj odpowiedzialne podejście do nauki.

Kryteria powodzenia

Ja wiem …

Rozumiem …

Mogę ….

Podczas zajęć

Wstęp – moment motywacyjny

Matematyka, przyjaciele,
Absolutnie każdy tego potrzebuje.
Pracuj pilnie na zajęciach
A sukces na pewno na Ciebie czeka!

Dzisiaj kontynuujemy naukę rozwiązywania równań i problemów metodą równań.

Aktualizowanie wiedzy

Aby wykonać zadania, dokonamy przeglądu podstawowych pojęć niezbędnych do rozwiązywania równań i problemów, które rozwiązuje się poprzez układanie równań.

( )

Jaki rodzaj równości nazywa się równaniem?

Jaką liczbę nazywamy pierwiastkiem równania?

Co to znaczy rozwiązać równanie?

Jak sprawdzić, czy równanie zostało poprawnie rozwiązane?

Sprawdzanie wykonania zadania domowego (Slajd nr 2)

(sprawdzenie odrobienia pracy domowej odbywa się za pomocą autotestu)

Rozwiązanie przez uczniów z wymową

(x – 87) – 27 = 36

87 – (41 + y) = 22

x – 87 = 36 + 27

41 + y = 87 - 22

x – 87 = 63

41 + y = 65

x = 63 + 87

y = 65 - 41

x = 150

y = 24

Badanie

(150 – 87) - = 36

87 – (41 + 24) = 22

63 – 27 = 36

87 – 65 = 22

36 = 36 (poprawnie)

22 = 22 (poprawnie)

Praca ustna

1.Wymień numery równań (równania są zapisane na tablicy), w których należy znaleźć dany wyraz.
W jakich równaniach odjemna jest nieznana?
W jakich równaniach należy znaleźć odejmowanie?
W jakich równaniach ten termin jest nieznany?
Znajdź pierwiastki równań.

x + 21 = 40; 2) a – 21 = 40; 3) 50 = a + 31; 4) s – 23 = 61; 5) 42 = 70 – y;

6) 38 - x = 38; 7) 25 – a = 25; 8) x + 32 = 32; 9) y – 0 = 27; 10) 60 – s = 35

(Slajd nr 3)

Praca grupowa
Znajdź nieznany numer:

1) Dodaliśmy 71 do niewiadomej i otrzymaliśmy 100.
(x + 71 = 100)
x = 100 – 71
x = 29
2) Iloczyn dwóch liczb wynosi 72, jeden czynnik to 12, znajdź drugi czynnik.
12*X = 72
X = 72:12
X = 6
3) Dzieląc określoną liczbę przez 9, iloraz wynosi 11. Znajdź tę liczbę.
x: 9 = 31
x = 31* 9
x = 279

Praca nad równaniami (slajd nr 5)

Uczniowie proszeni są o utworzenie trzech równań zgodnie z warunkami i rozwiązanie tych równań w następującej kolejności:
1) Różnica między sumą liczb „x” i 40 jest większa niż liczba 31 o 50.
(Równanie zostało rozwiązane z komentarzem)
2) Liczba 70 jest większa od sumy liczby 25 i „y” o 38.
(Uczniowie rozwiązują równanie samodzielnie, a jeden z uczniów zapisuje rozwiązanie na odwrocie tablicy)
3) Różnica między liczbą 120 a liczbą „a” jest mniejsza niż liczba 65 o 53.
(Rozwiązanie równania jest w całości zapisane na tablicy, po czym cała klasa omawia rozwiązanie równania)

Praca nad zadaniami (slajd nr 6)

Zadanie nr 1
W pudełku było kilka jabłek. Po włożeniu do niego kolejnych 32 jabłek było ich 81. Ile jabłek było pierwotnie w pudełku?

Co mówi problem? Jakie czynności wykonałeś z jabłkami? Co musisz wiedzieć o problemie? Co powinna reprezentować litera?
Niech w koszyku będzie x jabłek. Po włożeniu do niego kolejnych 32 jabłek, było (x + 32) jabłek, a zgodnie z warunkami zadania w koszyku było 81 jabłek.
Możemy więc stworzyć równanie:
x + 32 = 81,
x = 81 – 32,
x = 49

Początkowo w koszyku było 49 jabłek.
Odpowiedź: 49 jabłek.

Problem nr 2
Pracownia dysponowała 70 (m) tkaniny. Z części materiału uszyto sukienki, kolejne 18 (m) wykorzystano na spodnie, po czym pozostało 23 (m). Ile metrów materiału zużyto na sukienki?

Co mówi problem? Jakie czynności wykonałeś z tkaniną? Co musisz wiedzieć o problemie? Co powinna reprezentować litera?
Niech x (m) materiału zostanie użyte na sukienki. Następnie (x + 18) metrów materiału zużyto na uszycie sukienek i spodni. Z warunków zadania wiadomo, że zostało jeszcze 23 m.
Możemy więc stworzyć równanie:
70 – (x + 18) = 23,
x + 18 = 70 – 23,
x + 18 = 47,
x = 47 – 18,
x = 29.

Na sukienki zużyto 29 metrów materiału.
Odpowiedź: 29 metrów.

Niezależna praca (slajd nr 7)

Samodzielna praca oferowana jest studentom w dwóch opcjach.

1 opcja

Opcja 2

Rozwiąż równania:

1) 320 – x = 176

1) 450 – y = 246

2) y + 294 = 501

2) x + 386 = 602

Makarova T.P., szkoła średnia GBOU nr 618 Szkolenie „Równania” 5. klasa

Szkolenie dla klasy V na temat „Równania” w 2 wersjach

Makarowa Tatiana Pawłowna,

Nauczyciel, Szkoła Średnia nr 618, Moskwa

Kontyngent: klasa 5

Celem szkolenia jest sprawdzenie wiedzy i umiejętności studentów na temat „Równania”. Szkolenie przeznaczone jest dla uczniów klas V z podręcznika N.Ya Vilenkina, V.I. Zhokhova i innych. – M.: Mnemosyne, 2013. – 288 s. Test zawiera dwie równoległe opcje o jednakowym stopniu trudności, po dziewięć zadań każda (4 zadania wielokrotnego wyboru, 3 zadania z krótką odpowiedzią, 2 zadania z rozwiązaniem rozszerzonym).

Szkolenie to jest w pełni zgodne z federalnymi standardami edukacyjnymi (drugiej generacji), może być wykorzystywane podczas monitorowania zajęć w klasie, a także może być wykorzystywane przez uczniów klasy 5 do samodzielnej pracy nad tematem.

Na rozwiązanie testu przeznacza się od 15 do 25 minut lekcji. Klucze w zestawie.

Szkolenie dla klasy V na temat „Równania”. Opcja 1.

№p/s

Ćwiczenia

Odpowiedź

Rozwiązać równanie

574

1124

1114

1024

Znajdź pierwiastek równania

(156-X )+43=170.

1) Pierwiastkiem równania jest wartość litery.

2) Pierwiastek równania (23 – X) – 21 = 2 nie jest liczbą naturalną.

3) Aby znaleźć nieznany odjemnik, musisz odjąć różnicę od odejmowania.

4) Równanie x – x= 0 ma dokładnie jeden pierwiastek.

Petya pomyślał o liczbie. Jeśli dodasz 43 do tej liczby i dodasz 77 do powstałej kwoty, otrzymasz 258. Jaką liczbę miał na myśli Petya?

1) (X + 43) – 77 = 258

2) (X + 43) + 77 = 258

3) (X – 43) + 77 = 258

4) (X – 43) – 77 = 258

Rozwiąż równanie: (5· Z – 8) : 2 = 121: 11.

Rozwiąż równanie: 821 – ( M + 268) = 349.

Znajdź wartość liczby A, jeśli 8 A + 9X= 60 i X=4.

Rozwiąż zadanie za pomocą równania. Biblioteka posiadała 125 książek z zakresu matematyki. Po tym, jak uczniowie wzięli kilka książek i zwrócili 3 książki, było ich w sumie 116. Ile książek wzięli uczniowie?

Rozwiązać równanie:

456 + (X – 367) – 225 =898

Szkolenie dla klasy V na temat „Równania”. Opcja 2.

№p/s

Ćwiczenia

Odpowiedź

Część 1. Zadanie wielokrotnego wyboru

Rozwiązać równanie

525

1081

535

1071

Znajdź pierwiastek równania

942 – (y + 142) = 419.

391

481

1219

381

Wskaż numery prawidłowych stwierdzeń:

1) Równanie to równość zawierająca literę, której wartość należy znaleźć.

2) Pierwiastkiem równania jest dowolna liczba naturalna

3) Pierwiastkiem równania jest wartość litery, przy której z równania uzyskuje się prawidłowe wyrażenie liczbowe.

4) Aby znaleźć nieznaną dywidendę, musisz dodać dzielnik do ilorazu.

Dasha pomyślała o liczbie. Jeśli do tej liczby dodasz 43 i odejmiesz 77 od otrzymanej kwoty, otrzymasz 258. Jaką liczbę miał na myśli Dasha?

1) (X + 43) – 77 = 258

2) (X + 43) + 77 = 258

3) (X – 43) + 77 = 258

4) (X – 43) – 77 = 258

Część 2. Zadanie z krótką odpowiedzią

Rozwiąż równanie: 63: (2· X – 1) = 21: 3.

Rozwiąż równanie: 748 – ( B +248) = 300.

Znajdź wartość liczby A, jeśli 7 A – 3X= 41 i X=5.

Część 3. Zadania ze szczegółowymi rozwiązaniami

Rozwiąż zadanie za pomocą równania. W magazynie znajdowało się 197 maszyn. Po sprzedaniu części i sprowadzeniu 86 kolejnych w magazynie pozostało 115 maszyn. Ile maszyn sprzedano ogółem?

Równanie to równość, w której występuje nieznany wyraz – x. Trzeba znaleźć jego znaczenie.

Nieznana wielkość nazywana jest pierwiastkiem równania. Rozwiązanie równania oznacza znalezienie jego pierwiastka, a aby to zrobić, musisz znać właściwości równań. Równania dla klasy 5 nie są trudne, ale jeśli nauczysz się je poprawnie rozwiązywać, nie będziesz mieć z nimi problemów w przyszłości.

Główna właściwość równań

Kiedy obie strony równania zmienią się o tę samą wartość, nadal będzie to to samo równanie z tym samym pierwiastkiem. Rozwiążmy kilka przykładów, aby lepiej zrozumieć tę zasadę.

Jak rozwiązywać równania: dodawanie lub odejmowanie

Załóżmy, że mamy równanie w postaci:

a + x = b - tutaj a i b są liczbami, a x jest nieznanym składnikiem równania.

Jeżeli do obu stron równania dodamy (lub odejmiemy od nich) wartość c, to nie ulegnie ona zmianie:

za + x + do = b + do
za + x - do = b - do.

Przykład 1

Wykorzystajmy tę własność do rozwiązania równania:

37+x=51

Odejmij liczbę 37 od obu stron:

37+x-37=51-37

otrzymujemy:

x=51-37.

Pierwiastkiem równania jest x=14.

Jeśli przyjrzymy się uważnie ostatniemu równaniu, zobaczymy, że jest ono takie samo jak pierwsze. Po prostu przenieśliśmy wyraz 37 z jednej strony równania na drugą, zastępując plus minusem.

Okazuje się, że dowolną liczbę można przenieść z jednej części równania do drugiej o przeciwnym znaku.

Przykład 2

37+x=37+22

Wykonajmy tę samą czynność, przesuńmy liczbę 37 z lewej strony równania na prawą:

x=37-37+22

Ponieważ 37-37=0, po prostu zmniejszamy to i otrzymujemy:

x =22.

Identyczne wyrazy równania o tym samym znaku, znajdujące się w różnych częściach równania, można skrócić (przekreślić).

Mnożenie i dzielenie równań

Obie strony równości można również pomnożyć lub podzielić przez tę samą liczbę:

Jeśli równość a = b zostanie podzielona lub pomnożona przez c, nie ulegnie to zmianie:

a/c = b/c,
ac = bс.

Przykład 3

5x = 20

Podzielmy obie strony równania przez 5:

5x/5 = 20/5.

Ponieważ 5/5 = 1, zmniejszamy te mnożniki i dzielniki po lewej stronie równania i otrzymujemy:

x = 20/5, x = 4

Przykład 4

5x = 5a

Jeśli obie strony równania podzielimy przez 5, otrzymamy:

5x/5 = 5a/5.

Liczby 5 w liczniku i mianowniku lewej i prawej strony są anulowane, co daje x = a. Oznacza to, że identyczne czynniki po lewej i prawej stronie równań się znoszą.

Rozwiążmy inny przykład:

13 + 2x = 21

Wyraz 13 przesuwamy z lewej strony równania na prawą z przeciwnym znakiem:

2x = 21 - 13
2x = 8.

Dzieląc obie strony równania przez 2, otrzymujemy:

x = 4.

W tym filmie przeanalizujemy cały zestaw równań liniowych rozwiązywanych przy użyciu tego samego algorytmu - dlatego nazywane są one najprostszymi.

Najpierw zdefiniujmy: co to jest równanie liniowe i które nazywa się najprostszym?

Równanie liniowe to takie, w którym występuje tylko jedna zmienna i tylko do pierwszego stopnia.

Najprostsze równanie oznacza konstrukcję:

Wszystkie pozostałe równania liniowe sprowadzamy do najprostszych za pomocą algorytmu:

Rozwiń nawiasy, jeśli istnieją;
Przesuń terminy zawierające zmienną na jedną stronę znaku równości, a terminy bez zmiennej na drugą;
Podaj podobne wyrazy po lewej i prawej stronie znaku równości;
Podziel powstałe równanie przez współczynnik zmiennej $x$.

Oczywiście ten algorytm nie zawsze pomaga. Faktem jest, że czasem po tych wszystkich zabiegach współczynnik zmiennej $x$ okazuje się równy zeru. W takim przypadku możliwe są dwie opcje:

Równanie nie ma w ogóle rozwiązań. Na przykład, gdy okaże się, że $0\cdot x=8$, tj. po lewej stronie znajduje się zero, a po prawej stronie liczba różna od zera. W poniższym filmie przyjrzymy się kilku powodom, dla których taka sytuacja jest możliwa.
Rozwiązaniem są wszystkie liczby. Jest to możliwe tylko wtedy, gdy równanie zostało sprowadzone do konstrukcji $0\cdot x=0$. Jest całkiem logiczne, że niezależnie od tego, jakie $x$ podstawimy, i tak okaże się, że „zero jest równe zeru”, tj. poprawna równość liczbowa.

Zobaczmy teraz, jak to wszystko działa na przykładach z życia wziętych.

Przykłady rozwiązywania równań

Dziś mamy do czynienia z równaniami liniowymi i to tylko najprostszymi. Ogólnie równanie liniowe oznacza dowolną równość, która zawiera dokładnie jedną zmienną i dotyczy tylko pierwszego stopnia.

Takie konstrukcje rozwiązuje się w przybliżeniu w ten sam sposób:

Przede wszystkim należy rozwinąć nawiasy, jeśli takie istnieją (jak w naszym ostatnim przykładzie);
Następnie przynieś podobne
Na koniec wyizoluj zmienną, tj. przesuń wszystko, co jest związane ze zmienną – terminy, w jakich jest ona zawarta – na jedną stronę, a wszystko, co pozostaje bez niej, na drugą stronę.

Następnie z reguły trzeba podać podobne po każdej stronie powstałej równości, a potem pozostaje tylko podzielić przez współczynnik „x” i otrzymamy ostateczną odpowiedź.

W teorii wygląda to ładnie i prosto, ale w praktyce nawet doświadczeni uczniowie szkół średnich mogą popełniać obraźliwe błędy w dość prostych równaniach liniowych. Zazwyczaj błędy popełniane są podczas otwierania nawiasów lub przy obliczaniu „plusów” i „minusów”.

Ponadto zdarza się, że równanie liniowe w ogóle nie ma rozwiązań lub że rozwiązaniem jest cała oś liczbowa, tj. Jakikolwiek numer. Przyjrzymy się tym subtelnościom podczas dzisiejszej lekcji. Ale zaczniemy, jak już zrozumiałeś, od najprostszych zadań.

Schemat rozwiązywania prostych równań liniowych

Najpierw napiszę jeszcze raz cały schemat rozwiązywania najprostszych równań liniowych:

Rozwiń nawiasy, jeśli występują.
Izolujemy zmienne, tj. Przenosimy wszystko, co zawiera „X” na jedną stronę, a wszystko bez „X” na drugą.
Przedstawiamy podobne terminy.
Wszystko dzielimy przez współczynnik „x”.

Oczywiście ten schemat nie zawsze działa; są w nim pewne subtelności i sztuczki, a teraz je poznamy.

Rozwiązywanie rzeczywistych przykładów prostych równań liniowych

Zadanie nr 1

Pierwszy krok polega na otwarciu nawiasów. Ale nie ma ich w tym przykładzie, więc pomijamy ten krok. W drugim kroku musimy wyizolować zmienne. Uwaga: mówimy tylko o warunkach indywidualnych. Zapiszmy to:

Podobne terminy prezentujemy po lewej i prawej stronie, ale tutaj zostało to już zrobione. Dlatego przechodzimy do czwartego kroku: podziel przez współczynnik:

\[\frac(6x)(6)=-\frac(72)(6)\]

Więc otrzymaliśmy odpowiedź.

Zadanie nr 2

W tym zadaniu widzimy nawiasy, więc rozwińmy je:

Zarówno po lewej, jak i po prawej stronie widzimy mniej więcej ten sam projekt, ale postępujmy zgodnie z algorytmem, tj. oddzielanie zmiennych:

Oto kilka podobnych:

U jakich korzeni to działa? Odpowiedź: dla każdego. Zatem możemy napisać, że $x$ jest dowolną liczbą.

Zadanie nr 3

Trzecie równanie liniowe jest bardziej interesujące:

\[\lewo(6-x \prawo)+\lewo(12+x \prawo)-\lewo(3-2x \prawo)=15\]

Jest tu kilka nawiasów, ale nie są one przez nic mnożone, są po prostu poprzedzone różnymi znakami. Podzielmy je:

Wykonujemy drugi znany nam już krok:

\[-x+x+2x=15-6-12+3\]

Zróbmy matematykę:

Wykonujemy ostatni krok - dzielimy wszystko przez współczynnik „x”:

\[\frac(2x)(x)=\frac(0)(2)\]

O czym należy pamiętać przy rozwiązywaniu równań liniowych

Jeśli pominiemy zbyt proste zadania, chciałbym powiedzieć, co następuje:

Jak powiedziałem powyżej, nie każde równanie liniowe ma rozwiązanie - czasami po prostu nie ma pierwiastków;
Nawet jeśli są korzenie, może być wśród nich zero - nie ma w tym nic złego.

Zero to taka sama liczba jak pozostałe; nie powinieneś go w żaden sposób dyskryminować ani zakładać, że jeśli otrzymasz zero, oznacza to, że zrobiłeś coś złego.

Kolejna funkcja związana jest z otwieraniem nawiasów. Uwaga: jeśli przed nimi znajduje się „minus”, usuwamy go, ale w nawiasach zmieniamy znaki na naprzeciwko. A potem możemy go otworzyć za pomocą standardowych algorytmów: otrzymamy to, co widzieliśmy w powyższych obliczeniach.

Zrozumienie tego prostego faktu pomoże ci uniknąć popełniania głupich i bolesnych błędów w szkole średniej, gdy robienie takich rzeczy jest oczywiste.

Rozwiązywanie złożonych równań liniowych

Przejdźmy do bardziej złożonych równań. Teraz konstrukcje staną się bardziej złożone i przy wykonywaniu różnych przekształceń pojawi się funkcja kwadratowa. Nie powinniśmy się jednak tego bać, gdyż jeśli zgodnie z planem autora rozwiązujemy równanie liniowe, to w procesie transformacji wszystkie jednomiany zawierające funkcję kwadratową koniecznie się zniosą.

Przykład nr 1

Oczywiście pierwszym krokiem jest otwarcie nawiasów. Zróbmy to bardzo ostrożnie:

Przyjrzyjmy się teraz prywatności:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Oto kilka podobnych:

Oczywiście to równanie nie ma rozwiązań, więc napiszemy to w odpowiedzi:

\[\varnic\]

albo nie ma korzeni.

Przykład nr 2

Wykonujemy te same czynności. Pierwszy krok:

Przesuńmy wszystko ze zmienną w lewo, a bez niej - w prawo:

Oto kilka podobnych:

Oczywiście to równanie liniowe nie ma rozwiązania, więc zapiszemy je w ten sposób:

\[\varnic\],

albo nie ma korzeni.

Niuanse rozwiązania

Obydwa równania są całkowicie rozwiązane. Na przykładzie tych dwóch wyrażeń po raz kolejny przekonaliśmy się, że nawet w najprostszych równaniach liniowych wszystko może nie być takie proste: pierwiastków może być albo jeden, albo żaden, albo nieskończenie wiele pierwiastków. W naszym przypadku rozważaliśmy dwa równania, oba po prostu nie mają pierwiastków.

Chciałbym jednak zwrócić uwagę na inny fakt: jak pracować z nawiasami i jak je otwierać, jeśli przed nimi znajduje się znak minus. Rozważ to wyrażenie:

Przed otwarciem musisz pomnożyć wszystko przez „X”. Uwaga: mnoży się każdy indywidualny termin. Wewnątrz znajdują się dwa terminy - odpowiednio dwa terminy i pomnożone.

I dopiero po dokonaniu tych pozornie elementarnych, ale bardzo ważnych i niebezpiecznych przekształceń, można otworzyć nawias z punktu widzenia tego, że po nim znajduje się znak minus. Tak, tak: dopiero teraz, gdy przekształcenia zostaną zakończone, pamiętamy, że przed nawiasem jest znak minus, co oznacza, że wszystko poniżej po prostu zmienia znaki. Jednocześnie znikają same nawiasy i, co najważniejsze, znika również przedni „minus”.

To samo robimy z drugim równaniem:

To nie przypadek, że zwracam uwagę na te drobne, pozornie nieistotne fakty. Bo rozwiązywanie równań to zawsze ciąg elementarnych przekształceń, gdzie nieumiejętność jasnego i kompetentnego wykonania prostych czynności powoduje, że licealiści przychodzą do mnie i na nowo uczą się rozwiązywać takie proste równania.

Oczywiście nadejdzie dzień, w którym udoskonalisz te umiejętności do poziomu automatyzmu. Nie będziesz już musiał za każdym razem wykonywać tylu przekształceń; zapiszesz wszystko w jednej linii. Ale kiedy dopiero się uczysz, musisz napisać każdą akcję osobno.

Rozwiązywanie jeszcze bardziej złożonych równań liniowych

To, co teraz rozwiążemy, trudno nazwać najprostszym zadaniem, ale znaczenie pozostaje takie samo.

Zadanie nr 1

\[\lewo(7x+1 \prawo)\lewo(3x-1 \prawo)-21((x)^(2))=3\]

Pomnóżmy wszystkie elementy w pierwszej części:

Zadbajmy o prywatność:

Oto kilka podobnych:

Dokończmy ostatni krok:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Oto nasza ostateczna odpowiedź. I mimo że w rozwiązywaniu mieliśmy współczynniki z funkcją kwadratową, to znosiły się one nawzajem, przez co równanie było liniowe, a nie kwadratowe.

Zadanie nr 2

\[\lewo(1-4x \prawo)\lewo(1-3x \prawo)=6x\lewo(2x-1 \prawo)\]

Wykonajmy ostrożnie pierwszy krok: pomnóż każdy element z pierwszego nawiasu przez każdy element z drugiego. Po przekształceniach powinny powstać w sumie cztery nowe terminy:

Teraz ostrożnie wykonajmy mnożenie w każdym wyrazie:

Przesuńmy terminy z „X” w lewo, a te bez – w prawo:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Oto podobne terminy:

Po raz kolejny otrzymaliśmy ostateczną odpowiedź.

Niuanse rozwiązania

Najważniejsza uwaga dotycząca tych dwóch równań jest następująca: gdy tylko zaczniemy mnożyć nawiasy zawierające więcej niż jeden wyraz, robimy to według następującej zasady: pierwszy wyraz bierzemy z pierwszego i mnożymy przez każdy element z drugi; następnie bierzemy drugi element z pierwszego i podobnie mnożymy przez każdy element drugiego. W rezultacie będziemy mieli cztery kadencje.

O sumie algebraicznej

W tym ostatnim przykładzie chciałbym przypomnieć uczniom, czym jest suma algebraiczna. W matematyce klasycznej przez 1-7 dolarów rozumiemy prostą konstrukcję: odejmij siedem od jednego. W algebrze rozumiemy przez to: do liczby „jeden” dodajemy kolejną liczbę, a mianowicie „minus siedem”. Tym właśnie różni się suma algebraiczna od zwykłej sumy arytmetycznej.

Gdy tylko podczas wykonywania wszystkich przekształceń, każdego dodawania i mnożenia zaczniesz widzieć konstrukcje podobne do opisanych powyżej, po prostu nie będziesz miał żadnych problemów z algebrą podczas pracy z wielomianami i równaniami.

Na koniec spójrzmy na jeszcze kilka przykładów, które będą jeszcze bardziej złożone niż te, które właśnie sprawdziliśmy, i aby je rozwiązać, będziemy musieli nieco rozszerzyć nasz standardowy algorytm.

Rozwiązywanie równań z ułamkami

Aby rozwiązać takie zadania, będziemy musieli dodać do naszego algorytmu jeszcze jeden krok. Ale najpierw przypomnę Ci nasz algorytm:

Otwórz nawiasy.
Oddzielne zmienne.
Przynieś podobne.
Podziel przez stosunek.

Niestety, ten wspaniały algorytm, przy całej swojej skuteczności, okazuje się nie do końca odpowiedni, gdy mamy przed sobą ułamki. Jak zobaczymy poniżej, w obu równaniach mamy ułamek zarówno po lewej, jak i po prawej stronie.

Jak pracować w tym przypadku? Tak, to bardzo proste! Aby to zrobić, musisz dodać do algorytmu jeszcze jeden krok, który można wykonać zarówno przed, jak i po pierwszej akcji, a mianowicie pozbycie się ułamków. Zatem algorytm będzie następujący:

Pozbądź się ułamków.
Otwórz nawiasy.
Oddzielne zmienne.
Przynieś podobne.
Podziel przez stosunek.

Co to znaczy „pozbyć się ułamków”? Dlaczego można to zrobić zarówno po, jak i przed pierwszym standardowym krokiem? W rzeczywistości w naszym przypadku wszystkie ułamki są liczbowe w swoim mianowniku, tj. Wszędzie mianownik jest po prostu liczbą. Dlatego jeśli pomnożymy obie strony równania przez tę liczbę, pozbędziemy się ułamków.

Przykład nr 1

\[\frac(\lewo(2x+1 \prawo)\lewo(2x-3 \prawo))(4)=((x)^(2))-1\]

Pozbądźmy się ułamków w tym równaniu:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

Uwaga: wszystko jest mnożone raz przez „cztery”, tj. to, że masz dwa nawiasy, nie oznacza, że musisz pomnożyć każdy z nich przez „cztery”. Zapiszmy:

\[\lewo(2x+1 \prawo)\lewo(2x-3 \prawo)=\lewo(((x)^(2))-1 \prawo)\cdot 4\]

Teraz rozwińmy:

Wykluczamy zmienną:

Dokonujemy redukcji wyrazów podobnych:

\[-4x=-1\lewo| :\lewo(-4 \prawo) \prawo.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Otrzymaliśmy ostateczne rozwiązanie, przejdźmy do drugiego równania.

Przykład nr 2

\[\frac(\lewo(1-x \prawo)\lewo(1+5x \prawo))(5)+((x)^(2))=1\]

Tutaj wykonujemy te same czynności:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Problem jest rozwiązany.

Właściwie to wszystko, co chciałem wam dzisiaj powiedzieć.

Kluczowe punkty

Kluczowe ustalenia to:

Znać algorytm rozwiązywania równań liniowych.
Możliwość otwierania nawiasów.
Nie martw się, jeśli masz gdzieś funkcje kwadratowe, najprawdopodobniej zostaną one zredukowane w procesie dalszych przekształceń.
Istnieją trzy rodzaje pierwiastków w równaniach liniowych, nawet najprostszych: jeden pojedynczy pierwiastek, cała oś liczbowa jest pierwiastkiem i nie ma żadnych pierwiastków.

Mam nadzieję, że ta lekcja pomoże ci opanować prosty, ale bardzo ważny temat dla dalszego zrozumienia całej matematyki. Jeśli coś nie jest jasne, wejdź na stronę i rozwiąż przedstawione tam przykłady. Bądź na bieżąco, czeka Cię jeszcze wiele ciekawych rzeczy!

Równania liniowe. Rozwiązanie, przykłady.

Uwaga!
Są dodatkowe
materiały w sekcji specjalnej 555.
Dla tych, którzy są bardzo „nie bardzo…”
A dla tych, którzy „bardzo…”)

Równania liniowe.

Równania liniowe nie są najtrudniejszym tematem matematyki w szkole. Ale jest tam kilka sztuczek, które mogą zadziwić nawet wytrenowanego ucznia. Rozwiążmy to?)

Zazwyczaj równanie liniowe definiuje się jako równanie postaci:

topór + B = 0 Gdzie a i b– dowolne liczby.

2x + 7 = 0. Tutaj a=2, b=7

0,1x - 2,3 = 0 Tutaj a=0,1, b=-2,3

12x + 1/2 = 0 Tutaj a=12, b=1/2

Nic skomplikowanego, prawda? Zwłaszcza jeśli nie zauważysz słów: „gdzie aib są dowolnymi liczbami”... A jeśli zauważysz i beztrosko o tym pomyślisz?) W końcu jeśli a=0, b=0(możliwe są dowolne liczby?), wówczas otrzymujemy zabawne wyrażenie:

Ale to nie wszystko! Jeśli, powiedzmy, a=0, A b=5, Okazuje się to czymś całkowicie absurdalnym:

Co jest denerwujące i podważa zaufanie do matematyki, tak...) Zwłaszcza podczas egzaminów. Ale wśród tych dziwnych wyrażeń musisz także znaleźć X! Które w ogóle nie istnieje. I, co zaskakujące, ten X jest bardzo łatwy do znalezienia. Nauczymy się to robić. W tej lekcji.

Jak rozpoznać równanie liniowe po jego wyglądzie? To zależy od wyglądu.) Sztuczka polega na tym, że równania liniowe to nie tylko równania postaci topór + B = 0 , ale także dowolne równania, które można sprowadzić do tej postaci poprzez przekształcenia i uproszczenia. A kto wie, czy spadnie, czy nie?)

W niektórych przypadkach można wyraźnie rozpoznać równanie liniowe. Załóżmy, że mamy równanie, w którym są tylko niewiadome pierwszego stopnia i liczby. A w równaniu nie ma ułamki podzielone przez nieznany , to jest ważne! I dzielenie przez numer, lub ułamek liczbowy - zapraszamy! Na przykład:

To jest równanie liniowe. Są tu ułamki zwykłe, ale nie ma x w kwadracie, sześcianie itp. i nie ma x w mianownikach, tj. NIE dzielenie przez x. A oto równanie

nie można nazwać liniowym. Tutaj wszystkie X są w pierwszym stopniu, ale są dzielenie przez wyrażenie z x. Po uproszczeniu i przekształceniach możesz otrzymać równanie liniowe, równanie kwadratowe lub cokolwiek chcesz.

Okazuje się, że w jakimś skomplikowanym przykładzie nie da się rozpoznać równania liniowego, dopóki go prawie nie rozwiążesz. To jest denerwujące. Ale w zadaniach z reguły nie pytają o formę równania, prawda? Zadania wymagają równań decydować. To sprawia, że jestem szczęśliwy.)

Rozwiązywanie równań liniowych. Przykłady.

Całe rozwiązanie równań liniowych składa się z identycznych przekształceń równań. Swoją drogą, te przekształcenia (dwa z nich!) stanowią podstawę rozwiązań wszystkie równania matematyczne. Inaczej mówiąc rozwiązanie każdy równanie zaczyna się od tych właśnie przekształceń. W przypadku równań liniowych (rozwiązanie) opiera się na tych przekształceniach i kończy się pełną odpowiedzią. Warto skorzystać z linku, prawda?) Co więcej, są tam również przykłady rozwiązywania równań liniowych.

Najpierw spójrzmy na najprostszy przykład. Bez żadnych pułapek. Załóżmy, że musimy rozwiązać to równanie.

x - 3 = 2 - 4x

To jest równanie liniowe. Wszystkie X są ujęte w pierwszej potędze, nie ma dzielenia przez X. Ale tak naprawdę nie ma dla nas znaczenia, jakiego rodzaju jest to równanie. Musimy to rozwiązać. Schemat tutaj jest prosty. Zbierz wszystko, co ma X po lewej stronie równania, wszystko bez X (liczby) po prawej stronie.

Aby to zrobić, musisz przenieść - 4x w lewo, oczywiście ze zmianą znaku i - 3 - w prawo. Swoją drogą, to jest to pierwsze identyczne przekształcenie równań. Zaskoczony? Oznacza to, że nie kliknąłeś linku, ale na próżno...) Otrzymujemy:

x + 4x = 2 + 3

Oto podobne, uważamy:

Czego potrzebujemy do pełnego szczęścia? Tak, aby po lewej stronie znajdował się czysty X! Piątka stoi na przeszkodzie. Pozbycie się piątki z pomocą drugie identyczne przekształcenie równań. Mianowicie dzielimy obie strony równania przez 5. Otrzymujemy gotową odpowiedź:

Oczywiście elementarny przykład. To na rozgrzewkę.) Nie jest zbyt jasne, dlaczego zapamiętałem tutaj identyczne transformacje? OK. Weźmy byka za rogi.) Zdecydujmy się na coś solidniejszego.

Oto na przykład równanie:

Gdzie zaczynamy? Z X - w lewo, bez X - w prawo? Może tak być. Małe kroki na długiej drodze. Możesz też zrobić to od razu, w uniwersalny i skuteczny sposób. Jeśli oczywiście masz w swoim arsenale identyczne przekształcenia równań.

Zadam Ci kluczowe pytanie: Co najbardziej nie podoba Ci się w tym równaniu?

95 na 100 osób odpowie: ułamki ! Odpowiedź jest prawidłowa. Pozbądźmy się ich więc. Dlatego zaczynamy od razu druga transformacja tożsamości. Przez co należy pomnożyć ułamek po lewej stronie, aby mianownik został całkowicie zredukowany? Zgadza się, o 3. A po prawej? Przez 4. Ale matematyka pozwala nam pomnożyć obie strony przez ten sam numer. Jak możemy się wydostać? Pomnóżmy obie strony przez 12! Te. do wspólnego mianownika. Wtedy zarówno trzy, jak i cztery zostaną zmniejszone. Nie zapominaj, że musisz pomnożyć każdą część całkowicie. Oto jak wygląda pierwszy krok:

Rozszerzanie nawiasów:

Notatka! Licznik ułamka (x+2) Umieściłem to w nawiasie! Dzieje się tak, ponieważ przy mnożeniu ułamków mnożony jest cały licznik! Teraz możesz skrócić ułamki:

Rozwiń pozostałe nawiasy:

Nie przykład, ale czysta przyjemność!) Przypomnijmy sobie teraz zaklęcie z podstawówki: z X - w lewo, bez X - w prawo! I zastosuj tę transformację:

Oto kilka podobnych:

I podziel obie części przez 25, tj. ponownie zastosuj drugą transformację:

To wszystko. Odpowiedź: X=0,16

Uwaga: aby nadać oryginalnemu mylącemu równaniu odpowiednią formę, użyliśmy dwóch (tylko dwóch!) przemiany tożsamości– tłumaczenie lewo-prawo ze zmianą znaku i mnożeniem-dzieleniem równania przez tę samą liczbę. To uniwersalna metoda! Będziemy pracować w ten sposób z każdy równania! Absolutnie każdy. Dlatego cały czas żmudnie powtarzam o tych identycznych przemianach.)

Jak widać zasada rozwiązywania równań liniowych jest prosta. Bierzemy równanie i upraszczamy je za pomocą identycznych przekształceń, aż otrzymamy odpowiedź. Główne problemy dotyczą tutaj obliczeń, a nie zasady rozwiązania.

Ale... Przy rozwiązywaniu najbardziej elementarnych równań liniowych zdarzają się takie niespodzianki, że potrafią wprawić w silne odrętwienie...) Na szczęście takie niespodzianki mogą być tylko dwie. Nazwijmy je specjalnymi przypadkami.

Szczególne przypadki rozwiązywania równań liniowych.

Pierwsza niespodzianka.

Załóżmy, że natkniesz się na bardzo podstawowe równanie, na przykład:

2x+3=5x+5 - 3x - 2

Lekko znudzeni przesuwamy go z X w lewo, bez X - w prawo... Po zmianie znaku wszystko jest idealne... Otrzymujemy:

2x-5x+3x=5-2-3

Liczymy i... ups!!! Otrzymujemy:

Ta równość sama w sobie nie budzi zastrzeżeń. Zero naprawdę jest zerem. Ale brakuje X! I musimy zapisać w odpowiedzi, Ile wynosi x? Inaczej rozwiązanie się nie liczy, prawda...) Ślepy zaułek?

Spokój! W takich wątpliwych przypadkach mogą Cię uratować najbardziej ogólne zasady. Jak rozwiązywać równania? Co to znaczy rozwiązać równanie? To znaczy, znajdź wszystkie wartości x, które po podstawieniu do pierwotnego równania dadzą nam poprawną równość.

Ale mamy prawdziwą równość już stało się! 0=0, o ile dokładniejsze?! Pozostaje dowiedzieć się, przy którym x to się dzieje. Na jakie wartości X można podstawić oryginalny równanie, jeśli te x czy nadal zostaną zredukowane do zera? Pospiesz się?)

Tak!!! X można zastąpić każdy! Który chcesz? Co najmniej 5, co najmniej 0,05, co najmniej -220. Nadal będą się zmniejszać. Jeśli mi nie wierzysz, możesz to sprawdzić.) Zastąp dowolne wartości X oryginalny równanie i obliczenia. Cały czas będziesz dostawał czystą prawdę: 0=0, 2=2, -7,1=-7,1 i tak dalej.

Oto Twoja odpowiedź: x - dowolna liczba.

Odpowiedź można zapisać różnymi symbolami matematycznymi, istota się nie zmienia. Jest to całkowicie poprawna i pełna odpowiedź.

Druga niespodzianka.

Weźmy to samo elementarne równanie liniowe i zmieńmy w nim tylko jedną liczbę. Oto co zdecydujemy:

2x+1=5x+5 - 3x - 2

Po tych samych identycznych przekształceniach otrzymujemy coś intrygującego:

Lubię to. Rozwiązaliśmy równanie liniowe i otrzymaliśmy dziwną równość. W kategoriach matematycznych mamy fałszywa równość. Ale mówiąc prościej, nie jest to prawdą. Zachwycać się. Niemniej jednak ten nonsens jest bardzo dobrym powodem do prawidłowego rozwiązania równania.)

Znowu myślimy w oparciu o ogólne zasady. Co dadzą nam x, po podstawieniu do pierwotnego równania PRAWDA równość? Tak, żaden! Nie ma takich X. Bez względu na to, co włożysz, wszystko zostanie zredukowane, pozostaną tylko bzdury.)

Oto Twoja odpowiedź: nie ma rozwiązań.

To także całkowicie pełna odpowiedź. W matematyce często można znaleźć takie odpowiedzi.

Lubię to. Mam nadzieję, że zniknięcie X w procesie rozwiązywania dowolnego (nie tylko liniowego) równania nie wprawi Cię w żadne zamieszanie. To już znana sprawa.)

Teraz, gdy uporaliśmy się ze wszystkimi pułapkami równań liniowych, sensowne jest ich rozwiązanie.