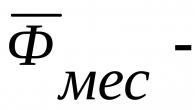Znamo da se tokom pravolinijskog kretanja smjer vektora brzine uvijek poklapa sa smjerom kretanja. Šta se može reći o smjeru brzine i pomaka pri zakrivljenom kretanju? Da bismo odgovorili na ovo pitanje, koristićemo istu tehniku ​​koju smo koristili u prethodnom poglavlju kada smo proučavali trenutnu brzinu pravolinijskog kretanja.

Slika 56 prikazuje određenu zakrivljenu putanju. Pretpostavimo da se tijelo kreće duž njega od tačke A do tačke B.

U ovom slučaju, put koji prolazi tijelo je luk A B, a njegov pomak je vektor. Naravno, ne može se pretpostaviti da je brzina tijela tijekom kretanja usmjerena duž vektora pomaka. Nacrtajmo niz tetiva između tačaka A i B (slika 57) i zamislimo da se kretanje tijela događa upravo duž ovih tetiva. Na svakom od njih tijelo se kreće pravolinijski, a vektor brzine je usmjeren duž tetive.

Učinimo sada naše ravne dijelove (korde) kraćim (slika 58). Kao i ranije, na svakom od njih vektor brzine je usmjeren duž tetive. Ali jasno je da je isprekidana linija na slici 58 već sličnija glatkoj krivulji.

Jasno je, dakle, da ćemo nastavljajući sa smanjivanjem dužine pravih odsječaka, takoreći, povući ih u tačke i izlomljena linija će se pretvoriti u glatku krivinu. Brzina u svakoj tački ove krive će biti usmjerena tangencijalno na krivulju u ovoj tački (Sl. 59).

Brzina kretanja tijela u bilo kojoj tački na krivolinijskoj putanji usmjerena je tangencijalno na putanju u toj tački.

U činjenicu da je brzina tačke pri krivolinijskom kretanju zaista usmjerena duž tangente, uvjerava se, na primjer, promatranje rada topa (slika 60). Ako krajeve čelične šipke pritisnete na rotirajući brusni kamen, vruće čestice koje silaze s kamena bit će vidljive u obliku iskri. Ove čestice lete brzinom kojom

posedovali su u trenutku odvajanja od kamena. Jasno se vidi da se pravac varnica uvek poklapa sa tangentom na kružnicu na mestu gde štap dodiruje kamen. Prskanje od točkova klizajućeg automobila takođe se kreće tangencijalno na krug (Sl. 61).

Dakle, trenutna brzina tijela u različitim tačkama krivolinijske putanje ima različite smjerove, kao što je prikazano na slici 62. Veličina brzine može biti ista u svim tačkama putanje (vidi sliku 62) ili varirati od tačke do tačke. tačka, od jednog trenutka do drugog (slika 63).

Koncepti brzine i ubrzanja prirodno su generalizirani na slučaj materijalne točke koja se kreće krivolinijska putanja. Položaj pokretne tačke na trajektoriji je određen radijus vektorom r povučen do ove tačke iz neke fiksne tačke O, na primjer, ishodište koordinata (slika 1.2). Neka u trenutku t materijalna tačka je na poziciji M sa radijus vektorom r = r (t). Nakon kratkog vremena D t, premjestit će se na poziciju M 1 sa radijusom - vektorom r 1 = r (t+ D t). Radijus - vektor materijalne tačke će dobiti prirast određen geometrijskom razlikom D r = r 1 - r . Prosječna brzina tokom vremena D t naziva se količina

Smjer prosječne brzine V sri utakmice sa vektorskim smjerom D r .

Ograničenje prosječne brzine u D t® 0, tj. derivacija radijusa - vektora r po vremenu

(1.9)

pozvao istinito ili instant brzina materijalne tačke. Vector V usmjereno tangencijalno na putanju pokretne tačke.

Ubrzanje A naziva se vektor jednak prvom izvodu vektora brzine V ili drugi izvod radijusa - vektor r po vremenu:

(1.10)

(1.11)

Zapazimo sljedeću formalnu analogiju između brzine i ubrzanja. Iz proizvoljne fiksne tačke O 1 nacrtaćemo vektor brzine V pokretna tačka u svim mogućim vremenima (slika 1.3).

Kraj vektora V pozvao tačka brzine. Geometrijski lokus tačaka brzine je kriva tzv hodograf brzine. Kada materijalna tačka opisuje putanju, odgovarajuća tačka brzine se kreće duž hodografa.

Rice. 1.2 razlikuje se od Sl. 1.3 samo notacijom. Radijus – vektor r zamijenjen vektorom brzine V , materijalna tačka - do tačke brzine, trajektorija - do hodografa. Matematičke operacije nad vektorom r pri pronalaženju brzine i iznad vektora V kada se pronađu, ubrzanja su potpuno identična.

Brzina V usmjerena duž tangencijalne putanje. Zbog toga ubrzanjea će biti usmjerena tangencijalno na hodograf brzine. To se može reći ubrzanje je brzina kretanja tačke brzine duž hodografa. dakle,

S obzirom na krivolinijsko kretanje tijela, vidjet ćemo da je njegova brzina različita u različitim trenucima. Čak iu slučaju kada se veličina brzine ne mijenja, još uvijek postoji promjena smjera brzine. U opštem slučaju, i veličina i smer brzine se menjaju.

Dakle, pri krivolinijskom kretanju brzina se kontinuirano mijenja, tako da se ovo kretanje odvija uz ubrzanje. Da bi se odredilo ovo ubrzanje (po veličini i smjeru), potrebno je pronaći promjenu brzine kao vektor, odnosno pronaći prirast veličine brzine i promjenu njenog smjera.

Rice. 49. Promjena brzine tokom zakrivljenog kretanja

Neka, na primjer, tačka, koja se kreće krivolinijski (slika 49), u nekom trenutku ima brzinu, a nakon kratkog vremenskog perioda - brzinu. Prirast brzine je razlika između vektora i . Pošto ovi vektori imaju različite smjerove, potrebno je uzeti njihovu vektorsku razliku. Povećanje brzine će biti izraženo vektorom predstavljenom stranom paralelograma sa dijagonalom i drugom stranom. Ubrzanje je omjer povećanja brzine i vremenskog perioda tokom kojeg se ovo povećanje dogodilo. To znači ubrzanje

Pravac se poklapa sa vektorom.

Odabirom dovoljno mali, dolazimo do koncepta trenutnog ubrzanja (up. § 16); kada je proizvoljan, vektor će predstavljati prosječno ubrzanje tokom određenog vremenskog perioda.

Smjer ubrzanja pri krivolinijskom kretanju se ne poklapa sa smjerom brzine, dok se za pravolinijsko kretanje ti pravci poklapaju (ili su suprotni). Za pronalaženje smjera ubrzanja za vrijeme krivolinijskog kretanja dovoljno je uporediti smjerove brzina u dvije bliske točke putanje. Budući da su brzine usmjerene tangente na putanju, onda se iz oblika same trajektorije može zaključiti u kojem smjeru je od putanje usmjereno ubrzanje. Zaista, budući da je razlika u brzinama u dvije bliske točke putanje uvijek usmjerena u smjeru gdje je putanja zakrivljena, to znači da je ubrzanje uvijek usmjereno prema udubljenosti putanje. Na primjer, kada se lopta kotrlja duž zakrivljenog žlijeba (slika 50), njeno ubrzanje u dijelovima i usmjereno je kao što je prikazano strelicama, a to ne ovisi o tome da li se lopta kotrlja od do ili u suprotnom smjeru.

Rice. 50. Ubrzanja tokom krivolinijskog kretanja su uvijek usmjerena prema udubljenosti putanje

Rice. 51. Izvesti formulu za centripetalno ubrzanje

Razmotrimo uniformno kretanje tačke duž krivolinijske putanje. Već znamo da je ovo ubrzano kretanje. Nađimo ubrzanje. Da biste to učinili, dovoljno je razmotriti ubrzanje za poseban slučaj ravnomjernog kretanja u krugu. Uzmimo dva bliska položaja i pokretnu tačku, razdvojene kratkim vremenskim periodom (Sl. 51, a). Brzine pokretne tačke u i jednake su po veličini, ali različite po pravcu. Nađimo razliku između ovih brzina pomoću pravila trougla (slika 51, b). Trokuti i su slični, poput jednakokračnih trokuta sa jednakim uglovima vrhova. Dužina stranice koja predstavlja povećanje brzine tokom određenog vremenskog perioda može se postaviti jednaka , gdje je modul željenog ubrzanja. Strana slična njoj je tetiva luka; Zbog male veličine luka, dužina njegove tetive se može uzeti približno jednakom dužini luka, tj. . dalje, ; , gdje je radijus putanje. Iz sličnosti trokuta slijedi da su omjeri sličnih stranica u njima jednaki:

odakle nalazimo modul željenog ubrzanja:

Smjer ubrzanja je okomit na tetivu. Za dovoljno kratke vremenske intervale možemo pretpostaviti da se tangenta na luk praktički poklapa s njegovom tetivom. To znači da se ubrzanje može smatrati usmjerenim okomito (normalno) na tangentu putanje, odnosno duž polumjera do centra kružnice. Stoga se takvo ubrzanje naziva normalno ili centripetalno ubrzanje.

Ako putanja nije kružnica, već proizvoljna kriva linija, tada u formuli (27.1) treba uzeti polumjer kružnice najbliže krivulji u datoj tački. Smjer normalnog ubrzanja u ovom slučaju će također biti okomit na tangentu putanje u datoj tački. Ako je za vrijeme krivolinijskog kretanja ubrzanje konstantno po veličini i smjeru, ono se može naći kao omjer prirasta brzine i vremenskog perioda tokom kojeg se ovo povećanje dogodilo, bez obzira na to koji vremenski period može biti. To znači da se u ovom slučaju ubrzanje može pronaći pomoću formule

slično formuli (17.1) za pravolinijsko kretanje sa konstantnim ubrzanjem. Ovdje je brzina tijela u početnom trenutku, a je brzina u trenutku vremena.

Znamo da se svako krivolinijsko kretanje događa pod utjecajem sile usmjerene pod uglom u odnosu na brzinu. U slučaju ravnomjernog kretanja po krugu, ovaj ugao će biti pravi. U stvari, ako, na primjer, rotirate lopticu vezanu za uže, tada je smjer brzine lopte u bilo kojem trenutku okomit na uže.

Sila zatezanja užeta, koji drži loptu na kružnici, usmjerena je duž užeta prema centru rotacije.

Prema drugom Newtonovom zakonu, ova sila će uzrokovati ubrzanje tijela u istom smjeru. Ubrzanje usmjereno radijalno prema centru rotacije naziva se centripetalno ubrzanje .

Izvedemo formulu za određivanje veličine centripetalnog ubrzanja.

Prije svega, imajte na umu da je kružno kretanje složeno kretanje. Pod uticajem centripetalne sile, telo se kreće ka centru rotacije i istovremeno se po inerciji udaljava od ovog centra tangencijalno na kružnicu.

Pretpostavimo da se za vrijeme t tijelo, koje se ravnomjerno kreće brzinom v, kretalo iz D u E. Pretpostavimo da bi u trenutku kada se tijelo nalazilo u tački D, centripetalna sila prestala da djeluje na njega. Tada bi se za vrijeme t pomjeralo u tačku K koja leži na tangenti DL. Ako bi u početnom trenutku tijelo bilo pod utjecajem samo jedne centripetalne sile (koja se ne kreće po inerciji), onda bi se za vrijeme t, kretajući se ravnomjerno ubrzano, pomjerilo u tačku F koja leži na pravoj DC. Kao rezultat sabiranja ova dva kretanja tokom vremena t, dobije se rezultujuće kretanje duž luka DE.

Centripetalna sila

Sila koja drži rotirajuće tijelo na kružnici i usmjerena je prema centru rotacije naziva se centripetalna sila .

Da biste dobili formulu za izračunavanje veličine centripetalne sile, trebate koristiti drugi Newtonov zakon, koji se primjenjuje na bilo koje krivolinijsko kretanje.

Zamjenom vrijednosti centripetalnog ubrzanja a = v 2 / R u formulu F = ma, dobivamo formulu za centripetalnu silu:

F = mv 2 / R

Veličina centripetalne sile jednaka je umnošku mase tijela puta kvadrata linearne brzine podijeljen s polumjerom.

Ako je data kutna brzina tijela, onda je prikladnije izračunati centripetalnu silu pomoću formule: F = m? 2 R, gdje? 2 R – centripetalno ubrzanje.

Iz prve formule jasno je da je pri istoj brzini, što je manji polumjer kružnice, veća je centripetalna sila. Dakle, na skretanjima na cesti tijelo koje se kreće (voz, automobil, bicikl) treba djelovati prema centru krivine, što je veća sila, to je skretanje oštrije, odnosno polumjer krivine je manji.

Centripetalna sila ovisi o linearnoj brzini: kako se brzina povećava, ona se povećava. Ovo je dobro poznato svim klizačima, skijašima i biciklistima: što se brže krećete, teže je skrenuti. Vozači vrlo dobro znaju koliko je opasno okretati automobil naglo pri velikoj brzini.

Linearna brzina

Centrifugalni mehanizmi

Kretanje tijela bačenog pod uglom u odnosu na horizontalu

Hajde da bacimo neko telo pod uglom prema horizontu. Posmatrajući njegovo kretanje, primijetit ćemo da se tijelo prvo podiže, krećući se po krivulji, a zatim i pada niz krivinu.

Ako usmjerite mlaz vode pod različitim uglovima prema horizontu, možete vidjeti da u početku, kako se kut povećava, mlaz udara sve dalje i dalje. Pod uglom od 45° prema horizontu (ako ne uzmete u obzir otpor vazduha) domet je najveći. Kako se kut dalje povećava, domet se smanjuje.

Da bismo konstruirali putanju tijela bačenog pod uglom u odnosu na horizont, nacrtamo horizontalnu pravu liniju OA i povučemo pravu liniju OS prema njoj pod datim uglom.

Na liniji OS na odabranoj skali postavljamo segmente koji su numerički jednaki putevima pređenim u smjeru bacanja (0–1, 1–2, 2–3, 3–4). Od tačaka 1, 2, 3, itd., spuštamo okomice na OA i na njih postavljamo segmente koji su numerički jednaki putevima koje prelazi slobodno padajuće tijelo za 1 s (1–I), 2 s (2–II ), 3 sec (3–III) itd. Povezujemo tačke 0, I, II, III, IV itd. glatkom krivom.

Putanja tijela je simetrična u odnosu na vertikalnu liniju koja prolazi kroz tačku IV.

Otpor zraka smanjuje i domet leta i maksimalnu visinu leta, a putanja postaje asimetrična. To su, na primjer, putanje granata i metaka. Na slici puna kriva šematski prikazuje putanju projektila u zraku, a tačkasta kriva u prostoru bez zraka. Koliko otpor zraka mijenja domet leta može se vidjeti iz sljedećeg primjera. U nedostatku otpora zraka, topovska granata kalibra 76 mm ispaljena pod uglom od 20° prema horizontu preletjela bi 24 km. U zraku ovaj projektil leti oko 7 km.

Njutnov treći zakon

Kretanje tijela bačenog horizontalno

Nezavisnost pokreta

Svako krivolinijsko kretanje je složeno kretanje koje se sastoji od kretanja po inerciji i kretanja pod utjecajem sile usmjerene pod uglom u odnosu na brzinu tijela. To se može pokazati u sljedećem primjeru.

Pretpostavimo da se lopta kreće duž stola jednoliko i pravolinijski. Kada se lopta otkotrlja sa stola, njena težina više nije uravnotežena silom pritiska stola i, po inerciji, održavajući jednolično i linearno kretanje, ona istovremeno počinje da pada. Kao rezultat dodavanja pokreta - ravnomjernih pravolinijskih po inerciji i jednoliko ubrzanih pod utjecajem gravitacije - lopta se kreće duž zakrivljene linije.

Eksperimentalno se može pokazati da su ovi pokreti nezavisni jedan od drugog.

Na slici je prikazana opruga koja, savijajući se pod udarom čekića, može jednu od loptica pokrenuti u horizontalnom smjeru i istovremeno osloboditi drugu loptu, tako da se obje počnu kretati u istom trenutku. : prvi duž krivine, drugi duž okomitog dolje. Obje lopte će udariti o pod u isto vrijeme; stoga je vrijeme pada obje lopte isto. Iz ovoga možemo zaključiti da kretanje lopte pod uticajem gravitacije ne zavisi od toga da li je lopta u početnom trenutku mirovala ili se kretala u horizontalnom pravcu.

Ovaj eksperiment ilustruje veoma važnu tačku u mehanici, tzv princip nezavisnosti pokreta.

Ujednačeno kretanje po krugu

Jedan od najjednostavnijih i najčešćih tipova krivolinijskog kretanja je ravnomjerno kretanje tijela u krugu. Na primjer, dijelovi zamašnjaka, tačke na zemljinoj površini kreću se po kružnici tokom dnevne rotacije Zemlje itd.

Hajde da uvedemo količine koje karakterišu ovo kretanje. Pogledajmo crtež. Pretpostavimo da kada se tijelo rotira, jedna od njegovih tačaka se kreće od A do B za vrijeme t. Radijus koji povezuje tačku A sa središtem kružnice rotira za ugao? (grčki “phi”). Brzina rotacije tačke može se okarakterisati veličinom omjera uglova? do vremena t, tj. ? /t.

Ugaona brzina

Odnos ugla rotacije poluprečnika koji povezuje pokretnu tačku sa centrom rotacije i vremenskog perioda tokom kojeg se ova rotacija dešava naziva se ugaona brzina.

Označavanje ugaone brzine grčkim slovom? (“omega”), možete napisati:

? = ? /t

Ugaona brzina je numerički jednaka kutu rotacije u jedinici vremena.

Kod ravnomjernog kretanja u krugu, ugaona brzina je konstantna veličina.

Prilikom izračunavanja ugaone brzine, ugao rotacije se obično meri u radijanima. Radijan je centralni ugao čija je dužina luka jednaka poluprečniku tog luka.

Kretanje tijela pod djelovanjem sile usmjerene pod uglom u odnosu na brzinu

Kada se razmatra pravolinijsko kretanje, postalo je poznato da ako sila djeluje na tijelo u smjeru kretanja, onda će kretanje tijela ostati pravolinijsko. Samo će se brzina promijeniti. Štoviše, ako se smjer sile poklapa sa smjerom brzine, kretanje će biti pravolinijsko i ubrzano. U slučaju suprotnog smjera sile, kretanje će biti ravno i sporo. To su, na primjer, kretanje tijela bačenog okomito naniže i kretanje tijela bačenog okomito prema gore.

Pogledajmo sada kako će se tijelo kretati pod utjecajem sile usmjerene pod uglom u odnosu na smjer brzine.

Pogledajmo prvo iskustvo. Napravimo putanju kretanja čelične kugle u blizini magneta. Odmah primjećujemo da se daleko od magneta loptica kretala pravolinijski, ali pri približavanju magnetu putanja kugle je bila savijena i lopta se kretala po krivulji. Smjer njegove brzine se stalno mijenjao. Razlog tome je djelovanje magneta na loptu.

Tijelo koje se pravolinijski kreće možemo učiniti da se kreće po krivulji ako ga gurnemo, povučemo za njega vezan konac i tako dalje, sve dok je sila usmjerena pod uglom u odnosu na brzinu kretanja tijela.

Dakle, krivolinijsko kretanje tijela nastaje pod djelovanjem sile usmjerene pod uglom u odnosu na smjer brzine tijela.

Ovisno o smjeru i veličini sile koja djeluje na tijelo, krivolinijski pokreti mogu biti vrlo raznoliki. Najjednostavniji tipovi krivolinijskih kretanja su kretanja u krugu, paraboli i elipsi.

Primjeri djelovanja centripetalne sile

U nekim slučajevima, centripetalna sila je rezultanta dvije sile koje djeluju na tijelo koje se kreće u krugu.

Pogledajmo nekoliko takvih primjera.

1. Automobil se kreće duž konkavnog mosta brzinom v, masa automobila je t, a poluprečnik zakrivljenosti mosta R. Kolika je sila pritiska koju automobil vrši na most u najnižoj tački?

Hajde da prvo ustanovimo koje sile deluju na automobil. Postoje dvije takve sile: težina automobila i sila pritiska mosta na automobil. (Snagu trenja u ovom i svim narednim pobjednicima isključujemo iz razmatranja).

Kada automobil miruje, ove sile, koje su jednake po veličini i usmjerene u suprotnim smjerovima, uravnotežuju jedna drugu.

Kada se automobil kreće duž mosta, tada, kao i na svako tijelo koje se kreće u krug, na njega djeluje centripetalna sila. Šta je izvor ove moći? Izvor ove sile može biti samo djelovanje mosta na automobil. Sila Q kojom most pritišće automobil koji se kreće ne samo da mora uravnotežiti težinu automobila P, već ga i prisiliti da se kreće u krug, stvarajući za to potrebnu centripetalnu silu F sile P i Q, jer je rezultat interakcije između vozila u pokretu i mosta.

Kinematika proučava kretanje bez identifikacije uzroka koji uzrokuju ovo kretanje. Kinematika je grana mehanike. Glavni zadatak kinematike je matematičko određivanje položaja i karakteristika kretanja tačaka ili tijela u vremenu.

Osnovne kinematičke veličine:

- Premjesti () – vektor koji povezuje početnu i krajnju tačku.

r – radijus vektor, određuje položaj MT u prostoru.

- Brzina– odnos puta i vremena .

- Put- skup tačaka kroz koje je tijelo prošlo.

- Ubrzanje - brzina promjene brzine, odnosno prvi izvod brzine.

2. Ubrzanje tokom zakrivljenog kretanja: normalno i tangencijalno ubrzanje. Ravna rotacija. Ugaona brzina, ubrzanje.

Krivolinijsko kretanje je kretanje čija je putanja kriva linija. Primjer krivolinijskog kretanja je kretanje planeta, kraj kazaljke na satu duž brojčanika, itd.

Krivolinijsko kretanje– ovo je uvek ubrzano kretanje. Odnosno, ubrzanje pri krivolinijskom kretanju je uvijek prisutno, čak i ako se modul brzine ne mijenja, već se mijenja samo smjer brzine.

Promjena brzine po jedinici vremena – ovo je tangencijalno ubrzanje:

Gdje su 𝛖 τ , 𝛖 0 vrijednosti brzine u trenutku t 0 + Δt i t 0, respektivno. Tangencijalno ubrzanje u datoj tački putanje smjer se poklapa sa smjerom brzine kretanja tijela ili mu je suprotan.

Normalno ubrzanje je promjena brzine u smjeru u jedinici vremena:

Normalno ubrzanje usmjerena duž polumjera zakrivljenosti putanje (prema osi rotacije). Normalno ubrzanje je okomito na smjer brzine.

Puno ubrzanje uz jednoliko promjenljivo krivolinijsko kretanje tijela jednako je:

-ugaona brzina pokazuje ugao kroz koji tačka rotira tokom ravnomernog kretanja u krugu u jedinici vremena. SI jedinica je rad/s.

Ravna rotacija je rotacija svih vektora brzina tačaka tijela u jednoj ravni.

3. Odnos između vektora brzine i ugaone brzine materijalne tačke. Normalno, tangencijalno i puno ubrzanje.

Tangencijalno (tangencijalno) ubrzanje– ovo je komponenta vektora ubrzanja usmjerena duž tangente na putanju u datoj tački putanje kretanja. Tangencijalno ubrzanje karakterizira promjenu brzine po modulu tokom krivolinijskog kretanja.

Normalno (centripetalno) ubrzanje je komponenta vektora ubrzanja usmjerena duž normale na putanju kretanja u datoj tački na putanji tijela. Odnosno, vektor normalnog ubrzanja je okomit na linearnu brzinu kretanja (vidi sliku 1.10). Normalno ubrzanje karakterizira promjenu brzine u smjeru i označava se slovom n. Vektor normalnog ubrzanja usmjeren je duž radijusa zakrivljenosti putanje.

Puno ubrzanje kod krivolinijskog kretanja sastoji se od tangencijalnog i normalnog ubrzanja prema pravilu vektorskog sabiranja i određuje se formulom.